La fonction logique OU Exclusif

Cette fonction est utilisée dans les domaines de l'électronique, de l'informatique (cryptographie) mais aussi en électricité (va-et-vient) et dans des dispositifs électromécaniques (contacteur inverseur). Elle est également appelée fonction XOR.

Etude de la fonction OU exclusif

Le OU EXCLUSIF (XOR) est une fonction obtenue avec un minimum de deux variables.
Elle correspond à V₆ du tableau des 16 fonctions à 2 variables.

Table de vérité

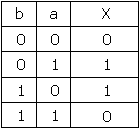
Considération 1

La fonction X prend une valeur égale à 1 quand l'une ou l'autre des variables, à l'exclusion des 2 à la fois, prennent une valeur égale à 1.
Nous l'écrivons : X = a ⊕ b.
Nous lirons : « X égale a xor b » ou bien « X égale a ou exclusif b ».

Considération 2

La fonction X prend une valeur égale à 1 quand :
a est égal à 1 ET b est inverse de 1
ou
a est inverse de 1 ET b est égale à 1.
Nous pouvons écrire : X = (a ⋅ b) + (a ⋅ b).

Ces deux considérations signifient que :
X = a ⊕ b = (a ⋅ b) + (a ⋅ b).

Nous remarquons que :
X = a quand b = 0 (fonction OUI)
X = a quand b = 1 (fonction NON).

La valeur de la variable b permet donc de choisir entre ses deux fonctions élémentaires ; Nous élaborons ainsi une fonction OUI ou une fonction inverseuse programmable.
Nous remarquons également que : X = 1 quand a ≠ b (inégalité) ce qui en fera du OU Exclusif une fonction de base pour l'élaboration de fonction ou circuit arithmétique.

Propriétés particulières :
a ⊕ 1 = a
a ⊕ 0 = a
a ⊕ a = 0
a ⊕ a = 1

Symbolisation

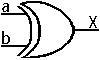
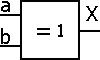
Forme canonique

X= a⊕b

Chronogramme

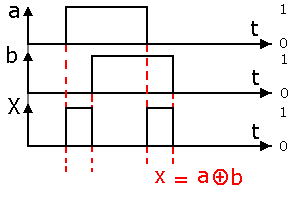
Exemples pratiques

CMOS : 4030, 4070
TTL : 7486, 74136.

Réalisation électrique

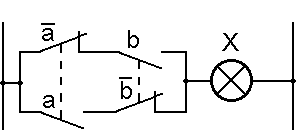
Utilisation en électricité industrielle : circuit d'exclusion mutuelle, démarrage moteur, démarrage étoile triangle…

En électronique et informatique : fabrication de front, codage biphasé Manchester…