Variable logique et algèbre de Boole
George Boole, mathématicien, logicien et un peu philosophe est né le 2 novembre 1815 à Lincoln, dans le Lincolnshire (Angleterre).
C'est le père fondateur de la logique moderne. En 1854 il réussi là où Leibniz avait échoué : allier en un même langage, mathématiques et symbolisme.

Le but : traduire des idées et des concepts en équations, leur appliquer certaines lois et retraduire le résultat en termes logiques.
Pour cela, George Boole crée une algèbre binaire n'acceptant que deux valeurs numériques : 0 et 1.
L'algèbre booléenne ou algèbre de Boole était née.
Les travaux théoriques de BOOLE, trouveront des applications primordiales dans des domaines aussi divers que les systèmes informatiques, les circuits électriques et téléphoniques, l'automatisme…
Notions de base
De nombreux dispositifs électroniques, électromécanique, mécaniques, électriques, pneumatiques, fonctionnement en tout ou rien.
Ceci sous-entend qu'ils peuvent prendre 2 états.
En voici quelques exemples :
- arrêt marche,
- ouvert fermé,
- enclenché déclenché,
- avant arrière,
- vrai faux,
- conduction blocage.
Pour ces raisons, il est beaucoup plus avantageux d'employer un système mathématique n'utilisant que 2 valeurs numériques (0 ou 1) pour étudier les conditions de fonctionnement de ces dispositifs
C'est le système binaire
L'ensemble des règles mathématiques qui pourront être utilisées avec des variables ne pouvant prendre que 2 valeurs possibles représente «l'agèbre de Boole»
Notion de variable binaire
La variable logique est une grandeur qui peut prendre 2 valeurs qui sont repérées habituellement 0 ou 1.
Cette variable est dite binaire et se note par une lettre comme en algèbre.
Exemple : a, b, x
Physiquement, cette variable peut correspondre à l'un des dispositifs cités ci-dessus dont les 2 états représentent les 2 valeurs possibles que peut prendre cette variable.
D'une façon générale, ces 2 états sont repérés «H» et «L» et nous attribuons :
- à l'état «H» (high) la valeur 1;
- à l'état «L»(low) la valeur 0.
On trouvera parfois cette notation du zéro ∅, pour éviter la confusion avec les lettres o ou O.
La variable binaire est aussi appelée variable booléenne.
Notion de fonction logique
Une fonction logique est le résultat de la combinaison (logique combinatoire) d'une ou plusieurs variables logiques reliées entre elles par des opérations et règles mathématiques booléennes bien définies :
- La valeur résultante de cette fonction dépend de la valeur des variables logiques, mais de toute façon cette résultante ne peut être que 0 ou 1.
- Une fonction logique possède donc une ou des variables logiques d'entrée et une variable logique de sortie.
- Cette fonction logique se note par une lettre comme en algèbre. Exemple : a, b, X ; c, d, Y.
Notion de logique combinatoire
La logique combinatoire, à l'aide de fonctions logiques, permet la construction d'un système combinatoire.
Un système est dit combinatoire quand il est de type boucle ouverte, c'est à dire qu'aucune des sorties n'est bouclée en tant qu'entrée.
A chaque combinaison d'entrée correspond une seule sortie.
Les systèmes combinatoires sont les plus simples et peuvent se représenter par une table de vérité indiquant pour chaque état d'entrée quel est l'état de sortie correspondant.
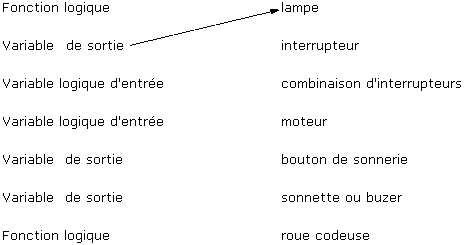
Exercice : faire correspondre, par des flèches, les termes de gauche avec les termes de droite