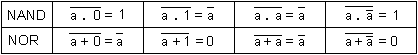Lois ou théorème de De Morgan
Auguste De Morgan est reconnu pour sa redécouverte de la loi de dualité entre la somme et le produit, où le contraire d'un agrégat (somme logique) est le composé (produit logique) des contraires des agrégants ; le contraire d'un composé est l'agrégat des contraires des composants.
Compléments logiques
Complément d'une somme logique
Complétons le tableau suivant et comparons les valeurs des fonctions Y1 et Y2.
| a | b | a + b | Y1 = a + b | a | b | Y2 = a . b |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Conclusion : a + b = a . b
Généralisation : Y = X1 + X2 + X3… + Xn = X1 ⋅ X2 ⋅ X3… ⋅ Xn
Complément d'un produit logique
Complétons le tableau suivant et comparons les valeurs des fonctions Y1 et Y2.
| a | b | a ⋅ b | Y1 = a ⋅ b | a | b | Y2 = a + b |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Conclusion : a ⋅ b = a + b
Généralisation : Y = X1 ⋅ X2 ⋅ X3… ⋅ Xn = X1 + X2 + X3… + Xn
Résumé
Le théorème de De MORGAN s'exprime par les deux relations :
a + b = a . b
a ⋅ b = a + b
Les simplifications fondamentales des fonctions logiques ET et OU sont dans le tableau suivant.
| Fonction | Simplifications | |||
|---|---|---|---|---|
| ET | a ⋅ 0 = 0 | a ⋅ 1 = a | a ⋅ a = a | a ⋅ a = 0 |
| OU | a + 0 = a | a + 1 = 1 | a + a = a | a + a = 1 |
Relation entre les opérations NOR et NAND
Nous pouvons démontrer que les opérations NOR et NAND ne sont pas distributives l'une pour l'autre.
Opération Nand
Nous déduisons que : a | (b ↓ c) = a + b + c ;
lire a nand (b nor c) est égal à : a barre ou b ou c . 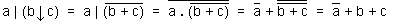
Nous déduisons également que : (a | b) ↓ (a | c) = a ⋅ b ⋅ c ;
lire (a nand b) nor (a nand c) est égal à : a et b et c . 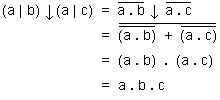
Nous constatons que les expressions a + b + c et a ⋅ b ⋅ c ne sont pas égales ;
il nous suffit de faire a = 0, b = 0, c = 0 pour le constater.
L'opération NAND n'est donc pas distributive par rapport à l'opération NOR.
Opération Nor
Nous déduisons que : a ↓ (b | c) = a ⋅ b ⋅ c ;
lire a nor (b nand c) est égal à : a barre et b et c . 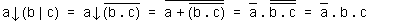
Nous déduisons également que : (a ↓ b) | (a ↓ c) = a + b + c ;
lire (a nor b) nand (a nor c) est égal à : a ou b ou c . 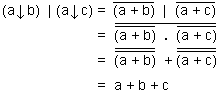
Nous constatons que les expressions a ⋅ b ⋅ c et a + b + c ne sont pas égales ;
il nous suffit de faire a = 1, b = 0, c = 0 pour le constater.
L'opération NOR n'est donc pas distributive par rapport à l'opération NAND.
Généralisation du théorème de De MORGAN
Si l'inverse de (a nand b) est égal à (a et b) (a | b = a ⋅ b),
et (a barre nor b barre) est équivalent à (a et b) (a ↓ b = a ⋅ b),
alors a | b = a ↓ b (1).
(voir les déductions détaillées sur l'image suivante). 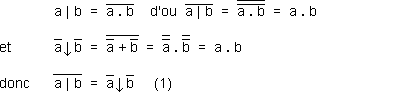
De même, si l'inverse de (a nor b) est égal à (a ou b) (a ↓ b = a + b),
et (a barre nand b barre) est équivalent à (a ou b) (a | b = a + b),
alors a ↓ b = a | b (2).
(voir les déductions détaillées sur l'image suivante).
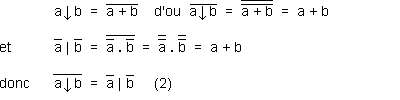
Conclusion
Les égalités (1) et (2) généralisent le théorème de MORGAN aux opérations NOR et NAND.
a | b = a ↓ b
a ↓ b = a | b
Les simplifications fondamentales des fonctions logiques NAND et NOR sont représentées dans l'image du tableau suivant.