Notions mathématiques pour l'électricité

Dès que l'on travail avec le courant alternatif sinusoïdal nous avons besoins d'autres connaissances mathématiques pour effectuer les calculs et études des circuits parcourus par ce type de courant.

Mesure des angles

Quelques symboles

• le radian s'écrit rad,
• cosinus s'écrit cos,
• sinus s'écrit sin,
• tangeante s'écrit tg,
• la constante pi (3,14159265359) se représente par la lettre de l'alphabet grec π,
• les degés par °,
• l'angle phi par φ.

Définition du radian (rad)

Considérons un cercle C de diamétre d et de rayon r.

Le radian est l'angle au centre qui intercepte entre ces deux côtés, sur la circonférence du cercle, une longueur d'arc égale au rayon de ce cercle.

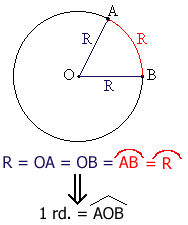
Considérons maintenant le périmétre du cercle ; P est le symbole du périmétre, mais nous utilisons L par commodité.

Si L = longueur ou périmètre du cercle et
si un cercle correspond un angle de 360°,
nous déduisons donc :

L=πd=2πr
comme r=rad
alors L=2πrad
d'ou : 2πrad=360°

Conversion de degré vers radian

Application 1

72° est égal à combien de radian ?

Nous posons 72°=72×2πrad⁄360
nous calculons que 72°=144⁢πrad⁄360
et le résultat de la simplification nous donne : 72°=2πrad⁄5

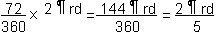
Conversion de radian vers degré :

Application 2

Combien font 13πrad⁄90 en degrés ?

Solution : comme rad=180°
alors 13×180⁄90=26°

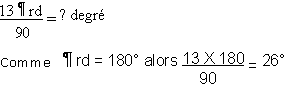
Trigonométrie

Rapports trigonométriques

Nous avons trois principaux rapports :

• Cosinus = Cos = côté adjacent/hypothénuse
• Sinus = Sin = côté opposé/hypothénuse
• Tangente = tg = côté opposé/côté adjacent

Ci-dessous l'illustration des rapports dans le triangle rectangle :

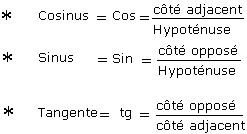
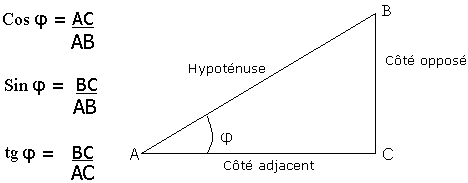
Notons quelques valeurs particulières :

• Sinus 45° = 0,707 soit (racine carrée de 2)/2,
• Cosinus 30° = 0,866 soit (racine carrée de 3)/2,
• Tangeante 60° = 1,732 soit racine carrée de 3,
• Tangeante 30° = 0,577 soit (racine carrée de 3)/3.

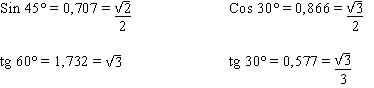
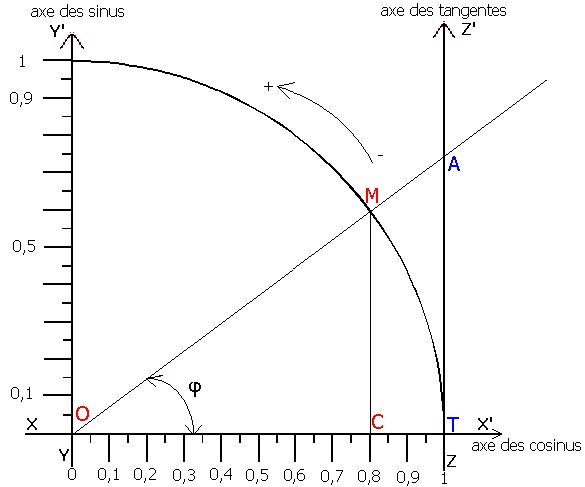
Cercle trigonométrique

Soit un cercle de centre O et de rayon égal à l'unité (exemple 1 dm) :
traçons les axes x x′ et y y′ passant par le centre du cercle
et traçons l'axe z z′ tangent au cercle ;
comptons positivement les angles à partir de OT et dans le sens anti-horaire (sens trigonométrique).

Dans le triangle rectangle OMC :
Cosφ = OC⁄OM = OC⁄1 = OC
L'axe x x′ est l'axe des cosinus

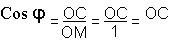
Sinφ = MC⁄OM = MC⁄1 = MC
L'axe y y′ est l'axe des sinus

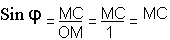
Dans le triangle rectangle OAT :
tgφ = AT⁄OT = AT⁄1 = AT
L'axe z z′ est donc l'axe des tangentes

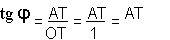
Ainsi par une lecture directe sur l'un des trois axes indiqués nous pouvons déterminer rapidement la valeur des rapports trigonométriques d'un angle.

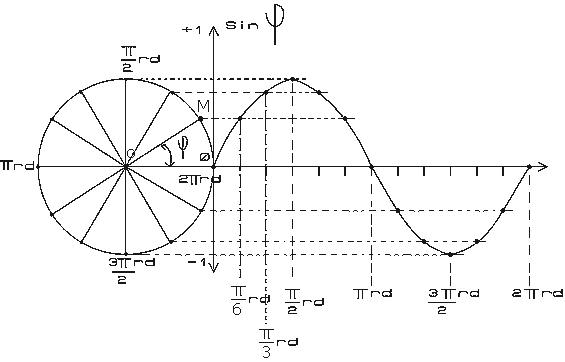
Tracé d'une sinusoïde

Puisque le point M peut décrire tout le cercle, l'angle phi peut donc prendre toutes les valeurs comprises entre 0 et 2πrd et nous pouvons remarquer alors que toutes les valeurs d'angle sont définies par leur sinus.
Nous pouvons donc représenter graphiquement les variations de sinus phi en fonction de l'angle.
La courbe ainsi obtenue se nomme une sinusoïde.