Les nombres à virgule fixe
La représentation de nombre en virgule flottante n'est pas la seule imaginable. Expliquons la représentation de nombre en virgule fixe par un exemple.
Représentation des nombres à virgule fixe
Soit (25,75)10 = (11001,110)2 
La position de la virgule est fixée arbitrairement à la 4ème case vers la gauche. La position de la virgule n'est pas visualisée.
La case la plus à droite représente le poids 20 : ce qui est évidemment faux.
Cette représentation suppose la multiplication implicite de ce nombre par 2-3
Le terme -3 est représentatif du positionnement fixe de la virgule. Il devra impérativement être mémorisé.
Comparaison des deux représentations (virgule fixe et virgule flottante)
Nous considérons avoir mémorisé le terme d'élévation à la puissance -3.
Si on travaille sur 10 positions, le nombre le plus élevé que l'on pourra écrire sera égal à :
en virgule fixe 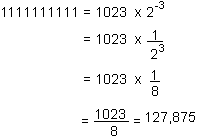
en virgule flottante 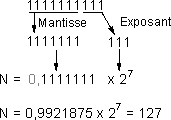
Par ailleurs, si nous voulons écrire un nombre inférieur à 1, par exemple 47/64 (0,734375) nous aurons :
7 chiffres significatifs en virgule flottante,
3 chiffres significatifs en virgule fixe.
en virgule fixe :
0 0 0 0 0 0 0 1 0 1
en virgule flottante :
1 0 1 1 1 1 0 0 0 0
Si l'on cherche l'équivalent décimal :
en virgule fixe :
101×2-3 = 1/2 + 1/8 = 40/64
en virgule flottante :
0,1011110×20 = (1/2 + 1/8 + 1/16 + 1/32 + 1/64 )×20 = 47/64
On s'aperçoit que la représentation en virgule fixe apporte une erreur qui peut, dans certains cas, ne pas être négligeable.
