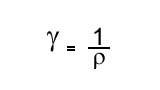Résistance et résistivité d'un conducteur
La résistance électrique d'un matériau est sa faculté d'empêcher le passage du courant électrique. La résistance se note R et se mesure en Ohm (symbole Ω).
Études pour caractériser un matériau conducteur et calculer la résistance d'un fil résistif.
Réalisons deux circuits électriques composés d'un ampèremètre, d'une lampe à filament et alimentés par le même générateur.
Expérience sur l'influence de la longueur
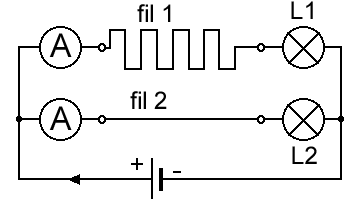
Expérience pour caractériser l'influence sur la longueur.
L1 éclaire moins que L2 car le courant circule moins dans le fil le plus long.
Dans le fil 1, les électrons ont un chemin plus long à parcourir. Ils rencontrent donc plus d'atomes qui les freinent sur leur parcours : la résistance d'un fil augmente quand sa longueur s'accroît.
Influence le la section
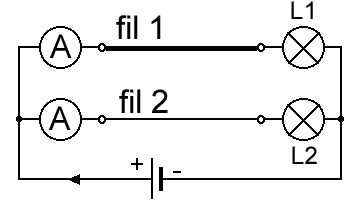
Expérience pour caractériser l'influence sur la section.
L2 éclaire moins que L1 car le courant circule avec plus de difficulté (donc moins) dans le fil le plus fin.
Dans le fil 1, les électrons sont plus dispersés et les chances de choc contre les atomes sont diminuées. Dans le fil 2 c'est le phénomène inverse : la résistance d'un fil augmente quand sa section diminue.
Influence de la nature du conducteur
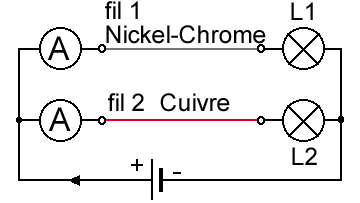
Expérience pour caractériser l'influence sur la nature des conducteurs.
L1 éclaire moins que L2 car le courant circule moins bien dans le fil de nickel-chrome.
La résistance d'un fil dépend donc de la nature du matériau.
Calcul de la résistance
Les mesures faites simultanément par OHM et POUILLET sur des conducteurs de section cylindrique ont conduit séparément ces deux savants à énoncer la loi suivante :
La résistance R d'un conducteur filiforme si sa section est constante est :
proportionnelle à sa longueur l,
inversement proportionnelle à sa section s,
variable avec la nature du conducteur.
Cette loi se traduit par la formule : R=ρ(l/s)
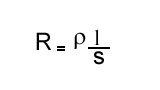
Formule de la résistance R, d'un conducteur filiforme de section constante.
Détail des unités :
l est en mètre,
s en m2,
ρ en Ω·m
R en Ω
ρ est un coefficient de proportionnalité qui exprime le pouvoir conducteur d'un matériau.
Pour simplifier, la valeur de la résistance est considérée indépendante du circuit dans lequel se trouve le matériau dont elle est constituée. En progressant dans les cours d'électricité nous apprendrons que des facteurs externes (type de courant, technologie de fabrication et température) peuvent influencer cette valeur.
A propos de la conductance
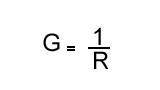
L'inverse de la résistance est la conductance (symbole G) elle s'exprime en Siemens, G=1/R.
Résistivité
La résistivité ρ (prononcer ro) est un coefficient qui caractérise la nature du conducteur ; elle se mesure en Ohm·mètre.
Plus la valeur de la résistivité est faible, plus le matériau est conducteur. Par exemple, la résistivité du fer est environ six fois plus grande que celle du cuivre ; nous en déduisons que le cuivre est six fois meilleur conducteur que le fer.
L'unité de résistivité d'un échantillon de conducteur pour R=1 Ω, l=1 m et s=1 m2 est égale à : ρ=R (s/l).
Formule de la résistivité d'un échantillon : rho=R (s/l)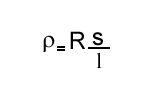
Avec :
ρ en Ω·m
R en Ω
s en m2
l en mètre
Valeurs usuelles de résistivités
- métaux usuels : ρ ±= 2·10-8 Ω·m
- semi-conducteur : 10-5 Ω·m < ρ < 109 Ω·m
- isolants : ρ > 109 Ω·m
Cas d'un conducteur de cuivre
La formule pratique est la suivante :
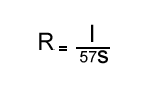
Formule pratique pour calculer la résistance d'un conducteur en cuivre à 15°C avec ρ ± 1,74 Ω·m, l en mètre et s en mm2.
Valeurs pour d'autres conducteurs
Tableau des résistivités des principaux conducteurs à 0 C° employés en électricité ou électronique.
α est le coefficient de température.
| Conducteurs | ρ en Ω·m | α |
|---|---|---|
| Aluminium | 2,733·10-8 | 4,03·10-3 |
| Argent | 1,629·10-8 | 3,85·10-3 |
| Bronze | 5,5·10-8 | |
| Cadmium | 6,8·10-8 | |
| Charbon | 40·10-8 | -0,4·10-9 |
| Constantan | 50·10-8 | 0 |
| Cuivre | 1,725·10-8 | 3,93·10-3 |
| Etain | 11,5·10-8 | |
| Fer | 9,98·10-8 | 6,5·10-3 |
| Laiton | 7,1·10-8 | |
| Maillechort | 30,0·10-8 | |
| Magnésium | 4,51·10-8 | |
| Manganin | 46,7·10-8 | |
| Mercure | 96,1·10-8 | |
| Nickel | 7,8·10-8 | 5,37·10-3 |
| Or | 2,271·10-8 | |
| Platine | 10,8 | |
| Plomb | 21,3·10-8 | |
| Tungstène | 5,44·10-8 | |
| Tantale | 13,5·10-8 | |
| Zinc | 6,06·10-8 |
Le constantan est un alliage de cuivre et de nickel (50 % à 60 % cuivre et 40 % à 50 % de nickel) que nous utilisons pour la fabrication de résistances de précision.
Résistivité de quelques isolants
| Isolant | Résistivité (Ω·m) |
|---|---|
| Eau pure | 1,8·105 |
| Verre | 1017 |
| Air | variable |
| Polystyrène | 1020 |
Conductivité
L'inverse de la résistivité s'appelle la conductivité (γ) : γ=1/ρ.
Formule de la conductivité : gamma=1/rho