Système de numération autoréférentiel
Publié le :
Le système de numération présenté ici a pour simple objectif d'inciter la reflexion, la recherche et invite toutes personnes à le faire évoluer pour le loisir de découvrir des nouveautés sur la théorie des nombres !
L'auteur, Ali Janati, précise que bien que non abouti (par exemple sur les nombres premiers) son système de numération est géométrique.
Numération géométrique
Le système se construit sur la base de cinq signes primitifs. La combinatoire obéissant à des règles d'assemblage de ces signes, a pour effet de construire de proche en proche des configurations permettant de représenter un nombre entier aussi grand que l'on désire.
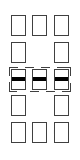
Le support de représentation est une case symbolisée par le rectangle suivant :
(rectangle vide).
Les cinq signes primitifs de base s'inscrivent donc à l'intérieur de cette case de la manière suivante :
| Signe | Correspondance |
|---|---|
| Barre inférieure | |
| Barre droite | |
| Barre supérieure | |
| Barre gauche | |
| Barre centrale |
Par son caractère spécifique de support d'écriture et de représentation de tous les signes et combinaisons de signes, la case vide sans barres est la représentation du nombre zéro (0).
Pour démarrer le mécanisme de calcul, posons que le nombre 1 est représenté par la barre inférieure : 1 → .
Addition de deux nombres
L'opération d'addition de deux nombres quelconques se fait par fusion graphique de cases. La fusion de deux cases en une troisième conserve par principe leurs contenus respectifs par « sommation graphique » des barres. Mais lorsque dans la fusion de cases une barre se superpose à elle-même, il y a effacement de cette barre et impression graphique dans la case résultante d'une barre à angle droit dans le sens contraire des aiguilles d'une montre.
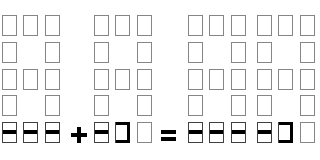
1+1=2 s'écrit : + =
L'impression de la barre droite comme résultat de la superposition-effacement de deux barres inférieures, représente le nombre 2.
Connaissant les représentations des nombres 1 et 2, il est possible de construire le nombre 3 dans le respect des règles définies précédemment :
1+2=3 s'écrit : + =
Il y a fusion de deux cases sans superposition de barres, d'où la conservation par sommation graphique des deux barres inférieures et droite et leur impression simultanée dans une seule et même troisième case représentant ainsi le nombre 3.
La similitude avec le système binaire est évidente. Avec cette différence près que dans le présent système au lieu de décaler indéfiniment les barres vers la gauche (comme pour les chiffres « 1 » alterné avec les chiffres « 0 ») nous faisons pivoter les barres en cercle fermé autour de la case.
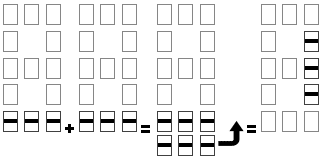
Pour former le nombre 4 nous pouvons aussi bien écrire :
1+3=4 soit + = que : 2+2=4 soit + = .
L'exploitation complète de toutes les configurations possibles permet de construire de proche en proche tous les nombres de 1 à 15 :
4+1=5 s'écrit : + = ,
5+1=6 s'écrit : + = …
Nous voyons sur le tableau ci-dessous toutes les constructions par addition du nombre 1 pour créer le chiffre suivant.
| Chif. | Rep. | Construction |
|---|---|---|
| 1 | ||
| 2 | 1+1=2 s'écrit : += | |
| 3 | 2+1=3 s'écrit : += | |
| 4 | 3+1=4 s'écrit : += | |
| 5 | 4+1=5 s'écrit : += | |
| 6 | 5+1=6 s'écrit : += | |
| 7 | 6+1=7 s'écrit : += | |
| 8 | 7+1=8 s'écrit : += | |
| 9 | 8+1=9 s'écrit : += | |
| 10 | 9+1=10 s'écrit : += | |
| 11 | 10+1=11 s'écrit : += | |
| 12 | 11+1=12 s'écrit : += | |
| 13 | 12+1=13 s'écrit : += | |
| 14 | 13+1=14 s'écrit : += | |
| 15 | 14+1=15 s'écrit : += |
La configuration représentant le nombre 15 est une configuration saturée. Toutes les possibilités ou combinatoires réalisables dans les règles de fusion de cases et de superpositions-effacement de barres sont épuisées. Il est techniquement impossible de rajouter un nombre quelconque au nombre 15 ( ) sans retomber sur un nombre qui se trouve déjà sur la liste.
Plus précisément,15 + 1 = 16 s'écrirait normalement d'après les règles fixées comme :
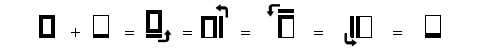
Processus tentant d'obtenir la somme de quinze plus un.
Ce qui nous fait retomber sur le nombre 1 et non sur le nombre 16 que nous ne savons pas encore écrire.
Pour échapper au cercle vicieux d'un formalisme qui revient continuellement à son point de départ, il est nécessaire d'introduire une règle de saturation de case par l'adjonction du cinquième et dernier signe primitif de base, à savoir : (barre centrale).
Cette règle de saturation de case exige que lorsqu'une opération de fusion de cases a pour effet de superposer deux barres gauches de boucler ainsi le tour complet de la case.

Boucle infinie de saturation d'une case.
Il y a effacement de celles-ci dans la case résultante et impression d'une barre à angle droit dans le sens contraire des aiguilles d'une montre, non pas dans la partie inférieure de la case (ce qui nous ferait retomber sur le nombre 1) mais dans sa partie centrale.
De ce fait, 15+1=16 s'écrit :
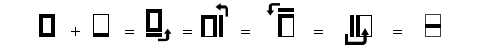
Processus d'écriture de la somme de 15+1.
De plus, lorsque le calcul d'addition le rend nécessaire, il y a création immédiate en deuxième position à droite d'une case supplémentaire :
12+7=19 s'écrit :
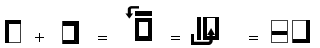
Ecriture de la somme de 12+7.
La superposition de la barre gauche sur elle même conduit à son propre effacement et à l'impression par saturation d'une barre centrale dans la case résultante. La configuration restante doit donc occuper une case placée immédiatement en deuxième position à droite, c'est à dire représentation finale du nombre 19.
De même, 8+15=23 s'écrit : + =
Il est immédiat qu'avec deux cases, il est possible d'écrire des nombres jusqu'à 32 dont la représentation sera le binôme .
Nous avons alors les correspondances suivantes :
| Chiffre | Représentation |
|---|---|
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| … | |
| 29 | |
| 30 | |
| 31 | |
| 32 |
Avec trois case il est possible d'écrire des nombres jusqu'à 48, dont la représentation sera le triplet .
En ce sens, 18+27=45 s'écrit : + = .
Au delà du nombre 48 un saut qualitatif doit intervenir dans cette mécanique de formalisation. Ce saut qualitatif est intrinsèque au système formel. Il permet de perpétuer son bouclage sur lui-même aux niveaux supérieurs de la représentation.
Car si nous voulons retrouver les mêmes principes de fusion de cases et de superposition-effacement de barres, comme il en était le cas avec la case (rectangle), nous devons à un moment donné casser ce développement linéaire et horizontal de cases les unes à la suite des autres.
De ce fait, il est techniquement nécessaire d'identifier un assemblage horizontal minimal de cases saturées, de considérer cet assemblage comme barre inférieure, puis l'intégrer à une « case composée » reproduisant exactement les caractéristiques formelles de la case unité .
L'assemblage minimal nécessaire et suffisant qui répond à ces conditions est le triplet qui conduit mécaniquement à la case composée :
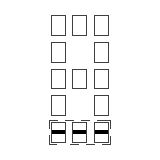
La case composée représentant la valeur 48 est équivalente graphiquement à (1).
Nous retrouvons ainsi à une échelle plus grande, notre case unité de départ avec une barre inférieure et qui représentait initialement le nombre 1.
La nouvelle matrice bidirectionnelle de représentation des nombres obtenue se prête formellement à l'application des règles de fusion de cases et de superposition-effacement de barres, comme il en été le cas pour la case unité , mais dans des proportions 48 fois plus grandes.
La case unité limitée à , devient une case composée et les barres inférieure, droite, supérieure, gauche et centrale sont représentées graphiquement par les figures ci-dessous.
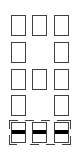
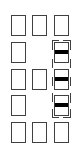
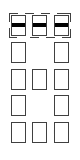
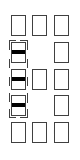
Les cases composées : barre inférieure (48), barre droite (96), barre supérieure (192), barre gauche (384), barre centrale (768).
Faisons la somme de 48 et d'un nombre compris entre 1 et 48 ;
48+23=71 est représenté graphiquement par la figure ci-dessous.
Addition de 48 et d'un nombre inférieur à 48.
Il y a fusion de cases mais on ne peut pas encore parler de superposition de barres car dans la deuxième case qui représente le nombre 23, la barre inférieure n'est pas complètement dessinée.
La barre inférieure de la première case étant saturée il y a donc seulement création immédiate d'une seconde case à droite de la première et impression des deux cases juxtaposées représentant le nombre 71.
Si maintenant nous faisons la somme 48+48=96.
Addition de 48 plus 48.
Dans ce cas il y a fusion de cases avec superposition de deux barres inférieures et donc impression à angle droit, dans le sens contraire des aiguilles d'une montre, d'une barre droite dans la case résultante.
Cette addition est graphiquement équivalente à + = = .
De même pour la somme 96+27=123 la représentation graphique est :
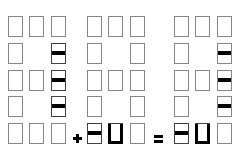
Addition de 96 plus 23.
Il y a fusion de cases sans superposition de barres et donc somme graphique des contenus respectifs des deux cases d'ou le nombre 123.
Une addition plus complexe du type 126+331=457.
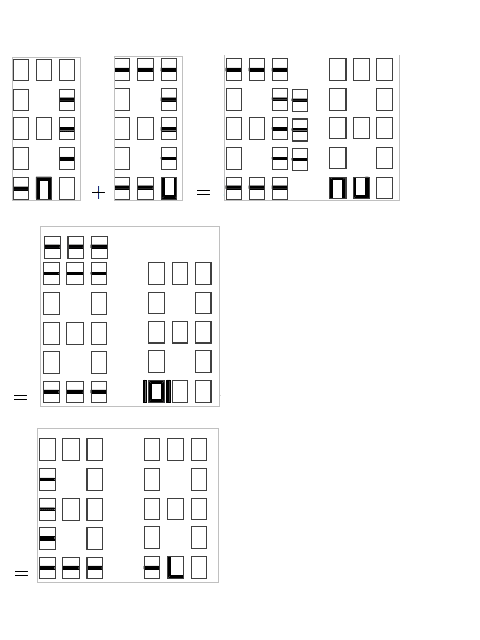
Addition de 126 plus 331.
Évolution hiérarchique du système
Le saut qualitatif de formalisation qui correspond pour l'essentiel à un emboîtement exponentiel de cases saturées (produit de 16 par des puissances croissantes de 48) confère à ce système aux niveaux hiérarchiques de circularité, la propriété d'être récursif. Nous obtenons par ce processus une fractale.
La case suivante sera de la forme :

Représentation de la fractale.
Le mécanisme de formalisation récursive se poursuivant ainsi, des nombres de plus en plus grands peuvent être représentés à travers des configurations s'auto complexifiant à l'infini. Et la lecture d'un nombre aussi grand soit-il devient une opération théorématique de reconnaissance de formes, c'est-à-dire, une reconnaissance des formes initiales, signes et combinaisons de signes primitifs situés à la base du système formel et choisis parmi les 16 premières configurations de celui-ci.
Exemple avec le nombre 14361
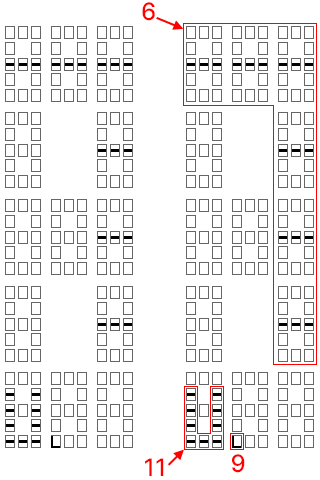
Représentation du nombre 14361.
La lecture récursive de la configuration obtenue permet d'identifier d'abord et au premier niveau de lecture la combinaison , puis à un second niveau de hiérarchie la combinaison , et enfin à une distance formelle extrêmement éloignée de la base, la configuration .
Nous reconnaissons les nombres 9, 11 et 6 tels qu'ils ont été formalisés à la base du système formel.
Conclusion
En conclusion nous sommes tentés de penser que ces configurations émergentes véhiculent une information d'ordre supérieur ou « méta-information » sur les propriétés arithmétiques du nombre considéré. C'est une intuition, mais il se peut que des recherches plus approfondies aboutissent à l'établissement de méta théorèmes sur le nombre considéré.
A propos
Le système de numération décrit ci-dessus est l'oeuvre exclusive et la propriété intellectuelle de son auteur, Ali JANATI, qui autorise sa publication par Positron-libre®.
Adaptation, mise en page pour le web et création des images et symboles SVG : Olivier Lejeune.