Les valeurs normalisées des séries de résistances
Les valeurs normalisées des résistances les plus utilisées se situent entre 10 ohms et 1 mégaohm. On utilise néanmoins des valeurs inférieures à l'ohm (résistances de mesure de courant) et des valeurs supérieures au mégaohm (résistances dans les montages haute tension ou à haute impédance).
Organisation des valeurs des résistances
Etant donné la diversité des applications, la précision des valeurs des résistances électroniques varie en fonction des dites applications.
C'est la raison pour laquelle la fabrication des résistances est organisée en série à l'intérieure d'une décade.
Série et décade
Une décade est un ensemble de valeurs dont les valeurs de résistance sont comprises entre un multiple de 1 et un multiple de 10 de l'unité considérée.
Exemple : 1 à 10 ohms ; 10 à 100 ohms ; 100 à 1000 ohms (1 kiloohms) ; 1 à 10 kiloohms ; 10 à 100 kiloohms ; 100 kiloohms à 1000 kiloohms (1 mégaohm)…
Une série représente le nombre de valeurs différentes que l'on dispose à l'intérieur d'une décade.
Pour la série E3, par exemple, nous avons trois valeurs possibles dans la décade : 1,0 2,2 et 4,7.
Soit les valeurs ohmiques possibles suivantes : 1,0 ohm ; 2,2 ohms ; 4,7 ohms ; 10 ohms ; 22 ohms ; 47 ohms ; 100 ohms ; 220 ohms ; 470 ohms ; 1 kiloohm ; 2,2 kiloohms…
Pour la série E12 nous avons 12 valeurs possibles par décade : 1,0 ; 1,2 ; 1,5 ; 1,8 ; 2,2 ; 2,7 ; 3,3 ; 3,9 ; 4,7 ; 5,6 ; 6,8 ; et 8,2.
Dans cette série E12 et pour les résistances dont la valeur est comprise entre 10 kΩ et 100 kΩ (décade 10kΩ à 100kΩ) , nous aurons :
10 kΩ ; 12 kΩ ; 15 kΩ ; 18 kΩ ; 22 kΩ ; 27 kΩ ; 33 kΩ ; 39 kΩ ; 47 kΩ ; 56 kΩ ; 68 kΩ et 82 kΩ.
Remarque : la série E12 n'étant plus fabriquée, elle est extraite de la série E24.
| Série | n par décade | n√10 | Tolérance | Observation |
|---|---|---|---|---|
| E3 | 3 | 2,15 | ±50 % | N'est plus utilisée |
| E6 | 6 | 1,47 | ±20 % | Ancien matériel à lampes |
| E12 | 12 | 1,21 | ±10 % | Extraite de la série E24 |
| E24 | 24 | 1,10 | ±5 % | Electronique grand public |
| E48 | 48 | 1,05 | ±2 % | Prototypage |
| E96 | 96 | 1,02 | ±1 % | Filtres BF et précision |
| E192 | 192 | 1,01 | ±0,5 % | Instrumentation |
La progression des valeurs des résistances
La progression des valeurs dans une série est géométrique.
La valeur de rang m de la série En est obtenue en posant :
n√10m
Mathématiquement n√x est égal à x(1÷n).
Par exemple, déterminons la 4ème valeur de la série E12 et calculons :
Val=12√104
Val=(104)(1÷12)
Val=104×(1÷12)
Val=10(4÷12)
Val=2,1544.
En arrondissant 2,1544 à 2,2 nous avons déterminer le 4ème élément de la série E12 (voir le tableau en bas de page).
C'est aussi le 8ème élément de la série E24 (24√108), le 2ème élément de la série E6 (6√102) et le 1er élément de la série E3 (3√101).
Cas spécifique ou n=m
La dernière valeur d'une série sera toujours égale à 10. Nous avons n=m
12√1012= 24√1024= n√10n= 10
Dans la pratique nous classerons souvent cette dernière valeur comme valeur de début de chaque décade.
Comment retrouver une valeur proche dans une série normalisée
Quand on calcule la valeur théorique d'une résistance, lors de la conception d'un circuit électronique, il peut être intéressant de retrouver la valeur pratique de la résistance à mettre en œuvre dans une série donnée.
Exemple
Le résultat « x » d'un calcul donne 6,73 ohms comme valeur de résistance.
Quelle est la valeur la plus proche dans la série « n » E24 ?
Il faut d'abord retrouver à quel rang « m » proche appartient cette valeur dans la série E24.
Avec x= 6,73,
n= 24,
m= ?
Calculons le rang : m= log xn
m= log(6,7324)= 19,87 ; nous arrondissons à 20.
La valeur la plus proche appartient au rang 20 de la série E24.
Calcul de la valeur : 24√1020=6,81 soit 6,8 Ω.
Précision ou tolérance
En augmentant le nombre de valeurs possibles dans une décade (3, 6, 12, 24, 48, 96), les valeurs de résistance se rapprochent de plus en plus.
Pour obtenir de plus en plus de valeurs proches les unes des autres, les constructeurs ont amélioré leurs procédés de fabrication et employé des matériaux fiables et stables dans le temps.
C'est de cette manière que nous avons obtenu des précisions différentes en fonction de la série utilisée.
La série E12 offre des valeurs de résistances précises à ±10 % et la série E96 à ±1 %.
Nous parlerons alors de tolérance à 10 %, 5 %, 1 %, etc.
Exemples de résistances de grande précision



Résistances de grande précision (0,01 % - 0,1 % - 1 %) du constructeur Powertron.
Crédit photo : www.powertron.de - extrait de datasheet pdf.
Valeurs normalisées E3 à E96
Tous les tableaux pratiques au format text/html sont disponibles à la page des tableaux des séries normalisées E3 à E96
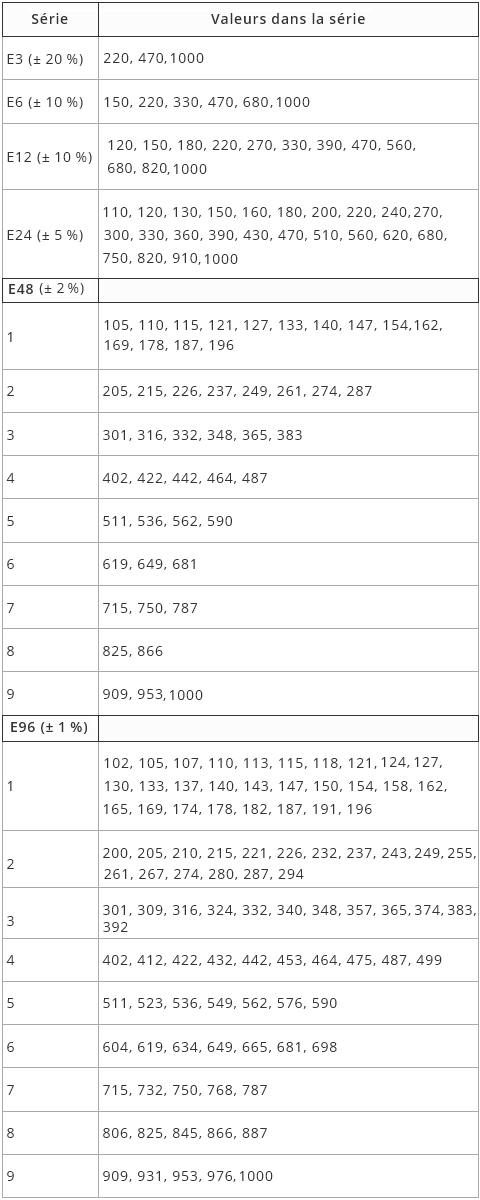
Tableau des séries normalisées E3 à E96.
