Les propriétés de l'algèbre de Boole

George Boole est le père fondateur de la logique moderne et son algèbre booléenne nous permet de résoudre les problèmes de logique combinatoire. Nous étudions ici les propriétés de cet algèbre de Boole : la commutativité, l'associativité et la distributivité.

Commutativité

Somme logique

X = a + b = b + a
fonction a ou b fonction b ou a

Produit logique

X = a . b = b . a
fonction a et b fonction b et a

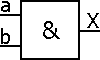
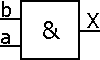
Associativité

Somme logique

X = a + b + c = (a + b) + c = a + (b + c)
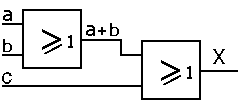
fonction a ou b ou c fonction (a ou b) ou c

Produit logique

X = a . b . c = (a . b) . c = a . (b . c)
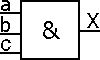
fonction a et b et c fonction (a et b) et c

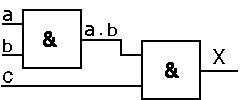
Distributivité

Produit logique

X = a . (b + c) = a . b + a . c
fonction a et b ou c fonction a et b ou a et c
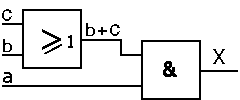
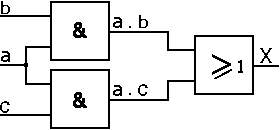
Exemple :
distributivité dun trajet
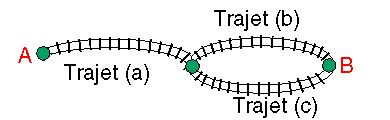
Trajet AB = (Trajet a) ET (Trajet b OU Trajet c)
Trajet AB = (Trajet a) ET (Trajet b) OU (Trajet a) ET (Trajet c)

Produit logique

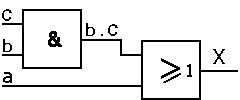
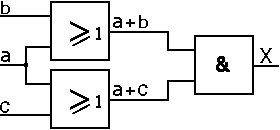
X = a + (b . c) = (a + b) . (a + c)
fonction a ou b et c fonction a ou b et a ou c
Exemple :
distributivité d'un moyen
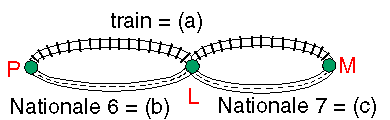
Trajet PLM = (Moyen a) OU (Moyen b ET Moyen c)
Trajet PLM = (Moyen a OU Moyen b) ET (Moyen a OU Moyen c)