Etapes de la résolution
Pour résoudre le problème il faut :
- Poser le problème correctement en envisageant tous les cas possibles, ce qui revient généralement
à mettre l'énoncé sous la forme d'une table de vérité
en faisant apparaître toutes les variables indépendantes d'entrées.
L'énoncé peut ne pas préciser l'état de sortie pour certaines combinaisons des variables, en raison des impossibilités technologiques, par exemples. - Etablir le tableau de Karnaugh correspondant.
Certaines cases peuvent ne correspondre ni à l'état 1, ni à l'état 0 de la grandeur de sortie. - Lire la fonction à partir du tableau en minimisant.
- Etablir le schéma.
L'établissement du schéma dépend de la technologie choisie pour la réalisation.
En électromécanique à relais, la fonction logique permet d'établir le schéma développé par la mise en série
ou parallèle des contacts.
En électronique ou en pneumatique, on dispose de blocs logiques correspondant aux fonctions de
base du type :
- Fonction NO,
- fonction OR,
- fonction AND,
- fonction NOR,
- fonction NAND.
Le montage sera réalisé soit par association des fonctions "NON" "OU" "ET", soit uniquement à l'aide de NAND ou uniquement à l'aide de NOR ; le schéma établi porte alors le nom de logigramme.
Établissement du logigramme
Avec des fonctions élémentaires ET, OU, NON
Soit la fonction :
Y = d + (a + b) c
Nous avons toujours intérêt à mettre la fonction sous la forme d'une somme de produits.
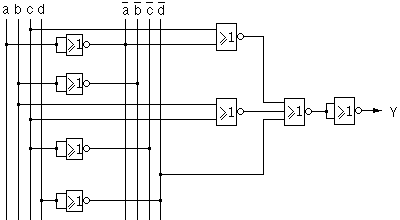
Y = a.c + b.c + d
Ce qui conduit au logigramme :
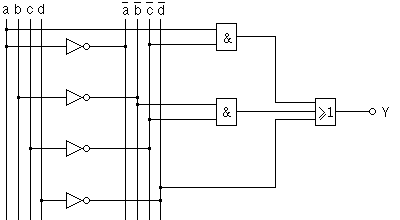
Avec des fonctions NAND
Présenter la fonction sous la forme d'une somme de produits (conforme au groupement des 1 dans le
diagramme de Karnaugh).
Méthode :
la fonction NAND de sortie est prise comme un OU,
les fonctions NAND d'entrée sont prises comme des ET.
Exemple :
Réalisation de la même fonction :
Y = d + (a + b) c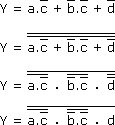
Ce qui conduit au logigramme :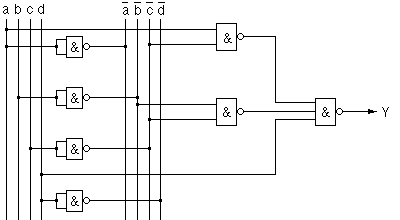
Remarque :
Toute fonction écrite sous la forme d'une somme de produits peut être réalisée en deux couches
d'opérateurs NAND.
Avec des fonctions NOR
Présenter la fonction sous la forme d'une somme de produits (conforme au groupement des 0 dans le
diagramme de Karnaugh).
Méthode :
la fonction NOR de sortie est prise comme un ET
les fonctions NOR d'entrée sont prises comme des OU.
Exemple :
réalisation de la même fonction :
Y = d + (a + b) c
Il faut mettre sous forme de circuit NOR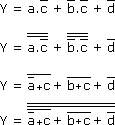
Ce qui nous conduit au logigramme suivant :
