Tableau de KARNAUGH

Nous avons vu que les règles et propriétés de l'algèbre de Boole permettent de simplifier les expressions logiques d'une fonction. Cette procédure est cependant relativement lourde et ne permet jamais de savoir si l'on aboutit à une expression minimale de la fonction ou pas. La méthode dite du tableau de Karnaugh allège et simplifie le travail du logicien.

La méthode inventée par Karnaugh

Nous pourrons utiliser la méthode du tableau de Karnaugh.
Dans le cas de deux variables binaires, nous avons quatre possibilités (ou combinaisons) à envisager que nous traduisons sous la forme de la table de vérité suivante :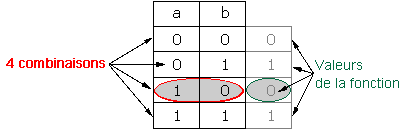

A chaque combinaison des variables est associée une valeur de la fonction.

Principes de simplification

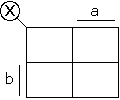
L'idée de KARNAUGH est d'associer une surface à chaque combinaison des variables, en adoptant la représentation suivante :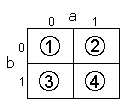

Nous disposons donc de 4 cases correspondant aux 4 combinaisons de variables.

La case 1 correspond à la combinaison a = 0 et b = 0 ⇒ (a . b )
La case 2 correspond à la combinaison a = 1 et b = 0 ⇒ (a ⋅ b )
La case 3 correspond à la combinaison a = 0 et b = 1 ⇒ (a ⋅ b )
La case 4 correspond à la combinaison a = 1 et b = 1 ⇒ (a ⋅ b )
Dans chacune de ces cases sera inscrite la valeur de la fonction pour la combinaison de variables correspondant à cette case.
En suivant l'exemple déjà représenté ci-dessus nous avons :
case 2 ⇒ combinaison de variables a = 1 et b = 0 ⇒ valeur de la fonction = 0.

Pour chacune des cases nous associons un produit de variables

Représentation d'un tableau de Karnaugh

Un tableau de Karnaugh peut se représenter sous les formes suivantes :

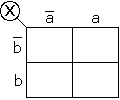
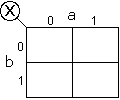
Ces trois représentations sont équivalentes.
Un tableau de Karnaugh nous renseigne donc sur les données suivantes :

• Le nom de la fonction (par ex : X),
• Le nom des variables (a, b),
• L'état des variables : 0 , 1 ou une barre représentant l'état 1,
• La valeur de la fonction (1 ou 0).

Nous notons que :
Dans la case 1 les variables valent toutes 0.
Si l'on adopte la notation algébrique booléenne pour les variables, elle nous renseigne du nom et de l'état de la variable ( a ; a ).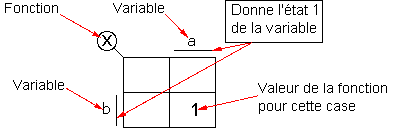

Tableau de karnaugh à 3 variables

A chaque case est associé un triplet des valeurs a, b, c.
Exemple : La case 1 représentera le triplet {0,0,0} ou a = 0, b = 0 et c = 0.
Nous pouvons dire également que la case 1 correspond au produit (a ⋅ b ⋅ c ).
Dans ce cas la représentation devient :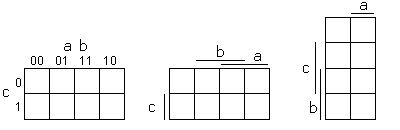

Tableau de Karnaugh à 4 variables

A chaque case est associé un quadruplet des valeurs a, b, c, d.
Exemples :
la case 4 représentera le quadruplet {1,0,0,0} ou a = 1, b = 0, c = 0 et d = 0 (a ⋅ b ⋅ c ⋅ d ).
La case 11 représentera le quadruplet {1,1,1,1} ou a = 1, b = 1, c = 1 et d = 1 (a ⋅ b ⋅ c ⋅ d ).
La case 16 représentera le quadruplet {1,0,1,0} ou a = 1, b = 0, c = 1 et d = 0 (a ⋅ b ⋅ c ⋅ d ).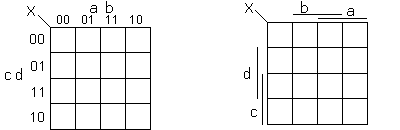

Adjacences des cases

Dans chaque cas, l'ordre d'écriture des états des variables fait qu'entre deux cases voisines (en ligne ou en colonne) une seule variable change d'état ; on dit de telles cases qu'elles sont adjacentes.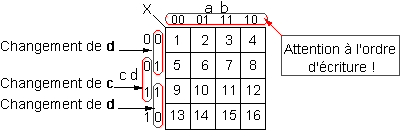

La case 2 correspond à a = 0 ; b = 1 ; c = 0 ; d = 0
La case 3 correspond à a = 1 ; b = 1 ; c = 0 ; d = 0
Lorsque nous passons de 2 à 3, seule la variable "a" change d'état :
2 et 3 sont adjacentes.
Lorsque nous passons de 2 à 1, seule la variable "b" change d'état :
2 et 1 sont adjacentes.
Lorsque nous passons de 2 à 6, seule la variable "d" change d'état :
2 et 6 sont adjacentes.
Enfin, lorsque nous passons de 2 à 14, seule la variable "c" change d'état :
2 et 14 sont adjacentes.
Nous venons de déterminer les adjacences de la case n° 2.
Cette notion de cases adjacentes est fondamentales.