Lecture d'une fonction logique dans un tableau de karnaugh
La lecture d'une fonction dans un tableau de karnaugh est le problème inverse du paragraphe précédent (voir Ecriture dans un tableau de Karnaugh).
Exercices de lecture
Nous pouvons lire successivement chacune des cases (fonction ET) et les lier par des fonctions OU.
Exemple 1
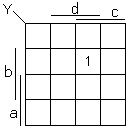
Dans l'exemple 1 nous lisons que Y est égale à a ET b ET c ET d
et nous écrivons Y = a ⋅ b ⋅ c ⋅ d.
Exemple 2
Oservons le tableau suivant :
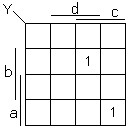
Dans l'exemple 2 nous lisons que :
Y est égale à a ET b ET c ET d OU a ET b ET C ET d
et nous écrivons Y = a ⋅ b ⋅ c ⋅ d + a ⋅ b ⋅ c ⋅ d
Regroupement de cases dans un tableau de Karnaugh
Soit le tableau de la fonction Y suivante :
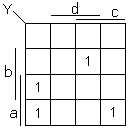
Nous pouvons écrire : 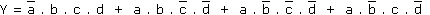
En fait, nous pouvons simplifier cette expression en remarquant que : 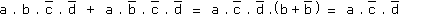
Ces deux termes correspondent à 2 cases adjacentes (cases 9 et 13).
Nous aurions pu lire directement dans le tableau de Karnaugh : 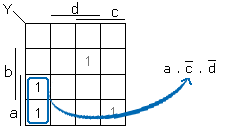
Notre expression est maintenant sous la forme : 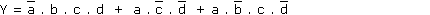
Minimisation d'une fonction dans un tableau de Karnaugh
En continuant notre observation nous pouvons remarquer également que la fontion vaut «1» dans deux autres cases adjacentes, ce qui nous aurait conduit à l'expression : 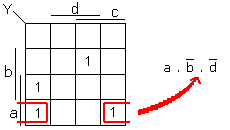
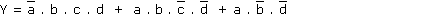
Mais l'expression la plus simple sera obtenue en regroupant les cases comme indiqué : 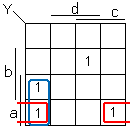
Ce qui correspond à la manipulation algébrique illustrée ci-après : 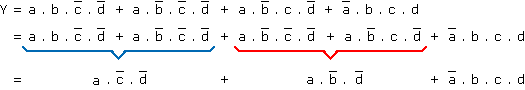
Ce qui donne l'expression la plus simple que l'on puisse obtenir :
Y = a ⋅ c ⋅ d + a ⋅ b ⋅ d + a ⋅ b ⋅ c ⋅ d
Nous avons minimiser l'équation de la fonction Y.
En regroupant les cases adjacentes par deux, on suprime une variable des termes correspondants ; une manipulation algébrique simple montre que pour supprimer deux variables, il faut disposer de 4 cases adjacentes, pour en supprimer 3 il faut 8 cases adjacentes…
Exemple
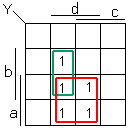
Y = a ⋅ d + b ⋅ c ⋅ d
Autre exemple
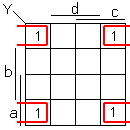
Y = b . d
Résumé
La méthode de lecture des fonctions dans un tableau de Karnaugh consiste donc à regrouper les cases adjacentes par 2n, n étant le plus grand possible. On essaie de regrouper toutes les cases de cette manière, les chevauchements de groupes étant permis.
Une zone de 8 cases définira une variable,
une zone de 4 cases définira un produit de 2 variables,
une zone de 2 cases définira un produit de 3 variables,
une zone d'1 cases définira un produit de 4 variables.
On lit enfin la fonction, en ne conservant pour chaque association que les variables qui ne changent pas d'état.
Cas particulier et élément indéterminé
Il arrive parfois qu'une fonction soit indéfinie pour certaines combinaisons des variables, pour différentes raisons ; la plus courante est que certaines combinaisons des variables étant impossibles, on ne juge pas utile de donner une valeur particulière à la fonction pour ces combinaisons là.
Dans les cases correspondantes du tableau de Karnaugh, on placera un signe particulier (∅ : élément indéterminé).
Lors du regroupement des cases nous transformons le ∅ en 0 ou en 1 suivant la convenance ou les simplifications qui peuvent en découler.
Exemple
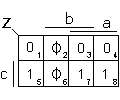
On obtient ici l'expression la plus simple de F en transformant le ∅ de la case 6 en «1» , ce qui permet de regrouper les cases 5, 6, 7, 8 et en transformant le ∅ de la case 2 en «0».
Nous aurons donc : Z = c
Voir la suite : Méthode de résolution d'un problème de logique combinatoire.
