Conversion et changement de base
Les conversions de nombre intervienent pour passer d'un système de numération vers un autre.
Conversion d'un nombre de base quelconque en nombre décimal
En exposant les principes des systèmes de numération de position, nous avons déjà vu comment convertir les nombres de base 8, base 2 et base 16 en nombres décimaux.
Conversion d'un nombre décimal en nombre binaire
Pour expliquer ce type de conversion, on peut revenir sur le système décimal.
Si nous divisons le nombre (543)10 par 10, nous obtenons comme quotient 54 et 3 comme reste. Cela signifie que ce nombre équivaut à :
(54×10) + 3
Le reste 3 est le chiffre indiquant le nombre d'unités.
En redivisant ce quotient (54) par 10, nous obtenons 5 comme deuxième quotient et 4 comme reste. Ce reste donne le deuxième chiffre du nombre, donc celui des dizaines.
Enfin, si l'on divise ce deuxième quotient par 10, nous obtenons 0 et il restera 5 qui représentera le chiffre des centaines. 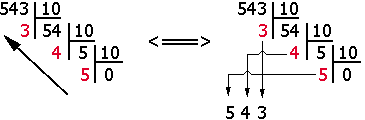
Résumer du principe de conversion
En divisant successivement un nombre par la base (10) et en ne conservant que les restes, on a réussi à exprimer le nombre par des chiffres inférieurs de 10. Mais attention, il faut lire les restes de bas en haut.
Conversion binaire
Maintenant si nous divisons un nombre décimal par 2, le quotient indique le nombre de fois que 2 est contenu dans ce nombre et le reste indique le chiffre des unités dans l'expression du nombre binaire.
Soit N le nombre, Q1 le quotient et R1 le reste, nous avons :
N = (Q1 × 2) + (R1 × 1)
N = (Q1 × 21) + (R1×20)
Exemple : 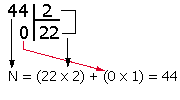
soit :
N = (22 × 2) + (0 × 1) = 44.
Pour obtenir l'expression binaire d'un nombre exprimé en décimal, il suffit de diviser successivement ce nombre par 2 jusqu'à ce que le
quotient obtenu soit égal à 0.
Comme pour la conversion dans le système décimal les restes de ces
divisions lus de bas en haut représentent le nombre binaire. 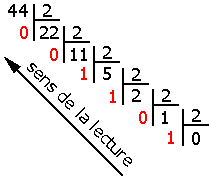
(44)10 = (101100)2.
Relation entre les nombres binaires et les nombres octaux
Exprimons (47)10 dans le système octal et le système binaire. Nous obtenons : 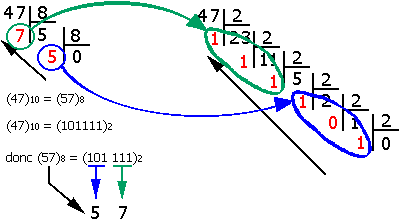
Nous pouvons remarquer qu'après 3 divisions en binaire nous avons le même quotient qu'après une seule en octal. De plus le premier reste en octal obtenu peut être mis en relation directe avec les trois premiers restes en binaire :
(111)2 = 1×22 + 1×21 + 1 × 20
(111)2 = 1 × 4 + 1 × 2 + 1 × 1
(111)2 = (7)8
et il en est de même pour le caractère octal suivant :
(101)2 = 1 × 22 + 0 × 21 + 1 × 20
(101)2 = 1 × 4 + 0 × 2 + 1 × 1
(101)2 = (5)8
Cette propriété d'équivalence entre chaque chiffre octal et chaque groupe de 3 chiffres binaires permet de passer facilement d'un système à base 8 à un système à base 2 et vice versa.
Exemple de conversion binaire octal et octal binaire
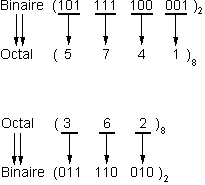
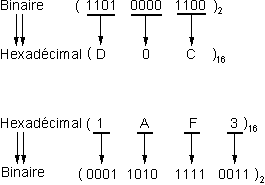
Relation entre les nombres binaires et les nombres hexadécimaux
La propriété d'équivalence que nous venons de voir entre le binaire et l'octal existe entre l'hexadécimal et le binaire.
La seule différence est qu'il faut exprimer chaque caractère hexadécimal à l'aide de 4 informations binaires.