Code binaire et décimal BCD 8421

Dans les systèmes numériques, l'entrée des données ne s'effectuent pas en pur code binaire. Ce sont plutôt des nombres décimaux codés en binaire (code BCD) qui sont utilisés.
A cet effet, il est possible de choisir n'importe qu'elle correspondance entre les nombres décimaux et les nombres binaires.

Les codes

Parmi la variété de codes possibles, le code « BCD 8421 » détient la première place. C'est la raison pour laquelle il est souvent appelé « code BCD » dans la littérature technique. Outre le code 8421, nous pouvons citer les codes décimaux connus : le « code 2421 », le « code plus 3 » (code excess 3) ou encore le « code Aiken ».
On distingue deux sortes de codes : les codes « pondérés » et les codes « non pondérés ».

Code binaire naturel

Ce code peut s'établir selon deux méthodes.
La première consiste à l'affectation d'une valeur de poids croissant à chaque colonne.
Pour chaque puissance de 2, nous épuisons en colonne toutes les combinaisons dans l'ordre croissant décimal, puis nous passons en ligne à la puissance de 2 immédiatement supérieure. Nous effectuons alors toujours dans le même ordre toutes les combinaisons jusqu'à épuisement…

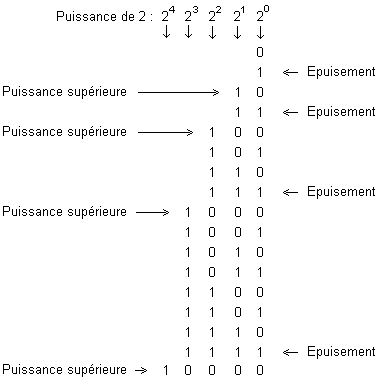
Une autre méthode consiste à établir une périodicité.
Chaque colonne correspond à une alternance de bits bien établie. Ainsi, en partant de la colonne de poids faible (ou LSB = Low Significant Bit) à la colone de poids fort (ou MSB = Most Significant Bit) nous avons une périodicité de 2, 4, 8, 16, 32… bits.

Attention à ne pas confondre périodicité et puissance de 2 !
Pour la colonne de périodicité de 2¹ (soit 2) nous avons une puissance de 2 égale à 2⁰ soit un poids binaire de 1
Pour la colonne de périodicité de 2² (soit une périodicité de 4) correspond une puissance de 2 égale à 2¹ soit un poids binaire de 2 …

Codes décimaux codés binaires (BCD)

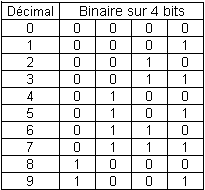
BCD (Décimal Codé en Binaire) signifie que les nombres décimaux 0 à 9 sont représentés par un nombre binaire à plusieurs chiffres.

La façon la plus simple de représenter les 10 chiffres décimaux par 4 variables binaires est de prendre les 10 premières combinaisons des 4 variables du système binaire naturel.

Si nous affectons les poids 1, 2, 4, 8 à ces 4 variables, nous obtenons le tableau de correspondance suivant :

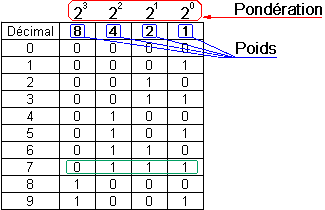
Le fait d'affecter des poids aux variables binaires nous conduit à appeler le code obtenu "code pondéré".
Ainsi le nombre le nombre 7 est représenté par la combinaison 0111 (7 = 0 + 4 + 2 + 1).
Le code 8421 (appelé aussi code 1248) est le plus simple des codes pondérés à 4 bits.
Voici quelques exemples de nombres représenté par le code 8421 :

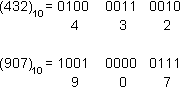
Remarques : un code est dit « pondérés » quand il existe des nombres qui indiquent le poids des chiffres binaires (voir Système de numération). En multipliant ces nombres par les chiffres binaires correspondants, on obtient l'équivalence décimale.
Tous les autres codes dans lesquels on ne peut repérer le poids des chiffres binaires sont appelés « non pondérés ». Ils sont élaborés sur une base à développement mathématique complexe ou plus simplement sont caractérisés par des tables faites spécialement.
Différents codes ont été imaginés, ayant diverses propriétés logiques et arithmétiques. Le choix de l'un ou de l'autre type de code dépend exclusivement des applications auxquelles il est destiné.

Convertisseur BCD 8421 vers décimal

Le code BCD 8421 représente chaque nombre décimal par un nombre binaire à 4 chiffres. La table de vérité représentée dans le tableau suivant montre la rapport entre le code BCD 8421 et le code décimal.

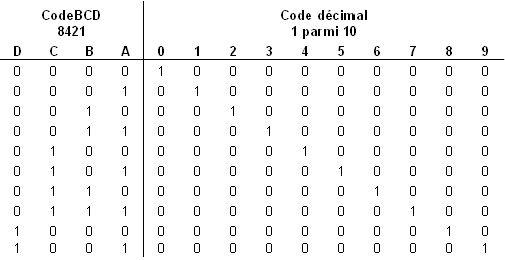
Comme l'illustre ce tableau, le code BCD 8421 ne comporte pas de combinaison plus grande que le 9 binaire (1001). C'est pourquoi, le circuit présente d'importantes simplifications. Le nombre 9, par exemple, est clairement représenté par le terme A.D (A ET D).
Lorsque A et D sont au niveau logique 1, B et C sont alors de niveau logique 0. Il n'y a pas de combinaison ABCD, ABCD ou ABCD.

Vous trouverez ci-après les équations simplifiées pour le décodeur BCD 1 parmi 10 :

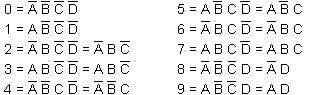
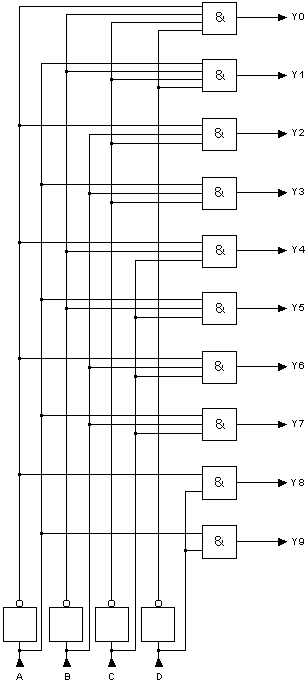
Le circuit de ce décodeur est représenté par le schéma suivant (la sortie est active au niveau logique 1 (logique positive)).

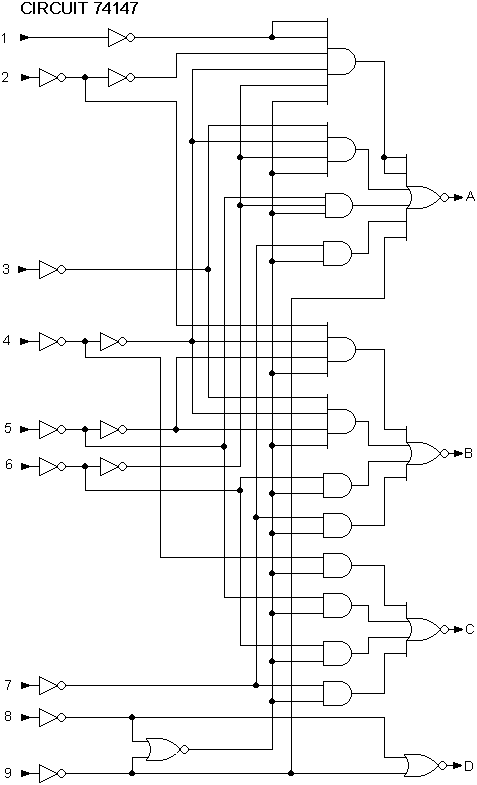
Exemple de circuit intégré : 74LS42.

Convertisseur décimal vers BCD 8421

Le convertisseur décimal BCD convertit le code 1 parmi 10 en code BCD 8421. Il est principalement utilisé sur les ordinateurs et autres systèmes numériques pour l'entrée de données : commutateur, touches, claviers…
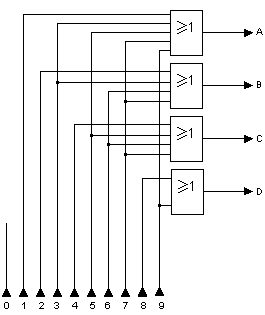
A partir du principe de correspondance des tableaux ci-dessus, nous obtenons les équations utiles à l'établissement du circuit :
A = 1 + 3 + 5 + 7 + 9
B = 2 + 3 + 6 + 7
C = 4 + 5 + 6 + 7
D = 8 + 9

Le schéma du circuit ci-dessous représente le principe d'un convertisseur décimal BCD. Dans ce circuit, si une des entrées 1 à 9 est de niveau logique 1, le nombre binaire associé apparaît aux sorties A à D. Pour le codage de la valeur décimale 0, aucune entrée particulière n'est nécessaire, étant donné que la sortie est zéro lorsque toutes les entrées sont au niveau logique 0.

Le convertisseur décimal BCD 8421 est disponible sous la forme d'un circuit intégré de type 74LS147. Ce circuit effectue un codage de priorité des niveaux logiques d'entrée de telle façon que seule l'entrée de rang le plus élevé est prise en compte.
Dans le cas d'un zéro décimal, toutes les entrées sont au niveau logique haut. En effet pour ce type d'encodeur, les entrées de données et les sorties sont actives au niveau logique bas.
Les entrées serons équipées d'un inverseur et les sorties d'une porte NOR. Le codage de la priorité est effectué avec un réseau de porte ET (plus quelques inverseurs) intercalé entre les inverseurs d'entrée et les NOR de sortie.