Codes, codeurs et transcodeurs
Un code est un langage composé de différents symboles ou mots. Pour transformer cette information « symbolique » en écriture binaire, nous avons besoin d'un codeur ou système de codage.
Notions de base
Quelques définitions
- Le codage est l'opération qui transforme une information (écriture décimal, position angulaire, vitesse, etc.) en écriture binaire dans un code de notre choix,
- un code est un un langage composé de différents symboles ou mots,
- un mot est un ensemble de caractères numériques ou alphanumériques,
- le transcodage est le passage d'un code à un autre.
Code binaire pur
Ce code correspond au système de numération binaire et fait référence au code binaire naturel.
Les caractères sont des bits.
Les mots sont formés par une association ou combinaison de bits. Avec n bits nous pouvons former au maximum 2n mots.
Codeurs à base de mécanique
Roue codeuse
Démontons une roue codeuse et observons les diverses pièces constitutives.


Elle est constituée d'une «galette» de circuit imprimé qui tourne mécaniquement.
Sur cette galette sont gravées plusieurs pistes en partie conductrices (cuivre doré).

Sur ces pistes viennent s'établir des contacts électriques.


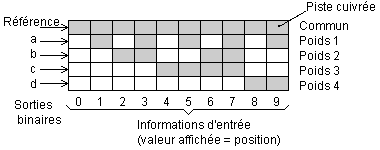
La représentation d'une galette de roue codeuse en vue rectiligne est la suivante (10 positions codées en binaire pur).
Codeur de position
En automatisme la position d'un organe peut être directement fournie par un codeur généralement en code Gray.
Par exemple un disque de codage de position angulaire solidaire d'un arbre (voir la page consacrée au code Gray).
Codeur électronique
Les informations analogiques (températures, pression, humidité…) sont acquises sous forme de tension ou courant proportionnel par des capteurs ad hoc. Cette tension ou ce courant seront ensuite convertis en informations binaires suivant le code binaire pur à l'aide d'un circuit électronique.

Circuit de transcodage
Dans le traitement des signaux numériques, les transcodeurs sont utilisés pour adapter les différents codes numériques les uns par rapport aux autres.
Ils effectuent la conversion d'une numération déterminée en une autre.
La conversion d'un résultat de calcul binaire dans le code à 7 segments pour un afficheur numérique est un exemples parmi d'autres.
Outre les principes fondamentaux des transcodeurs, les informations suivantes sont ici pour donner quelques exemples de circuit de transcodage pour les codes connus, tels que le code BCD, le code plus 3, le code Gray…
Principe de base des transcodeurs
Les transcodeurs sont des circuits qui convertissent les différents codes entre eux. D'une manière générale, nous pouvons définir le transcodage comme étant la représentation d'un élément de l'ensemble A par un ou plusieurs éléments pris dans un ensemble B d'éléments. Le rapport entre les deux quantités est déterminé par une règle de correspondance.
La représentation numérique la plus connue et la plus répandue en technique numérique est le code binaire. Pour une meilleur lisibilité, le code binaire peut être reproduit en code octal (chaque triplet de chiffres binaire est écris en nombre décimal). Parmi les autres codes nous citerons : les nombres BCD (nombres décimaux codés en binaire), le code Aiken, le code plus 3, le code Gray, le code 1 parmi 10…
Chaque code présente deux attributs caractéristiques : la longueur m et le nombre de mot de code n possible.
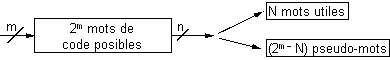
Pour le code BCD, par exemple, la longueur est m=4 et le nombre de mots de code (mots utiles) N=10.
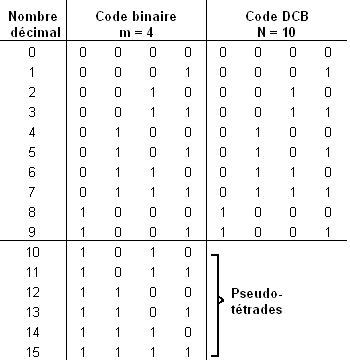
Il faut prendre en considération la différence entre un code complet et un code incomplet. Le code complet contient tous les mots de code binaire ou combinaisons possibles. Par contre, le code incomplet n'utilise qu'une partie des combinaisons possibles.
Le code BCD fait donc partie du groupe des codes incomplets étant donné qu'il n'utilise que 10 mots de code binaire possibles sur 16.
Décodeurs et encodeurs
Selon leur mode de fonctionnement les transcodeurs sont subdivisés en décodeurs et encodeurs.
Les décodeurs convertissent un code d'entrée de longueur m en code de sortie de 1 parmi n.
Pour les lignes d'entrée codées en binaire, il y a 2m = n mots de code possibles et donc n lignes de sortie.
Exemple d'un décodeur 1 parmi 4 :
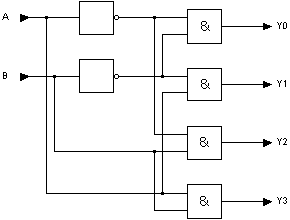
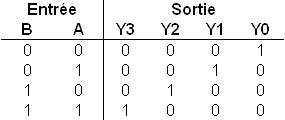
Sur le circuit de décodage illustré ci-dessus, la sortie active délivre un niveau logique 1, toutes les autres sorties étant de niveau logique 0.
Si nous souhaitons avoir une sortie active à l'état bas, il suffit de remplacer les quatre portes ET par des portes NON ET (nand).
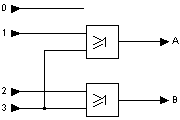
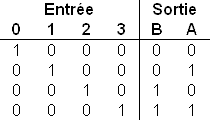
Les codeurs convertissent un code d'entrée 1 parmi n en un code de sortie de longueur m. Pour n lignes d'entrée, il y a m lignes de sortie pour un signal codé en binaire.
Exemple d'un codeur simple avec des portes OU :