Code 2421
Le code 2421 permet de représenter une valeur numérique inférieure ou égale à 9 avec 4 bits ; Le 0(10) se représente 0000 et le 9(10) 1111.
Parmi la variété de codes possibles, le code 2421 est également utilisé. Dans ce code, les poids affectés aux variables binaires ne sont plus 8, 4, 2, 1 mais 2, 4, 2, 1.
Le tableau suivant nous présente une comparaison entre le code 2421 et le 8421.
| Nombre décimal | Code 8421 | Code 2421 | ||||||
|---|---|---|---|---|---|---|---|---|
| 8 | 4 | 2 | 1 | 2 | 4 | 2 | 1 | |
| D | C | B | A | D' | C' | B' | A' | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
Dans ce code il existe deux manières de représenter certain chiffres.
Ainsi, 7 peut s'écrire : 0111 ou 1101
et 5 : 0101 ou 1011.
La première représentation est étudier dans cette page, la seconde est connu sous le nom de code 2421 AIKEN.
Nous pouvons remarquer également que le 9 en décimal est représenté par quatre bits à 1 dans le code 2421. Ce qui veut dire que l'on ne peut pas représenter une valeur supérieure à 9 avec 4 bits en 2421 contrairement au code 8421 qui peut représenter 16 valeurs différentes.
Convertisseur 2421 décimal
Le code 2421 n'a pas fait l'objet d'une version circuit intégré. Le circuit pourra être câblé en technologie discrète avec des fonctions ET et INVERSEUSE.
Mais l'intégration en dur d'un tel convertisseur est possible avec un CPLD ou FPGA. Nous pouvons décrire notre circuit intégré graphiquement avec un outils traditionnel de CAO permettant de connecter ensemble les portes élémentaires nécessaires.
La description textuelle par un langage de description de type VHDL est aussi une possibilité non négligeable et d'actualité.
Nous pouvons alors disposer d'un convertisseur de code 2421 vers décimal sous la forme d'une brique logiciel réutilisable à l'infini.
La totalité des 16 combinaisons à 4 bits n'étant pas utilisées il est possible de faire des économies de plusieurs fonctions logiques. Les équations logiques du convertisseur de code 2421 décimal seront les suivantes :
0 = A'⋅B'⋅C',
1 = A'⋅B'⋅C',
2 = A'⋅B'⋅C',
3 = A'⋅B'⋅C',
4 = A'⋅B'⋅C',
5 = A'⋅B'⋅C',
6 = A'⋅B'⋅C'⋅D',
7 = A'⋅B'⋅C'⋅D',
8 = A'⋅D',
9 = A'⋅D'.
Le schéma de ce convertisseur de code est le suivant :
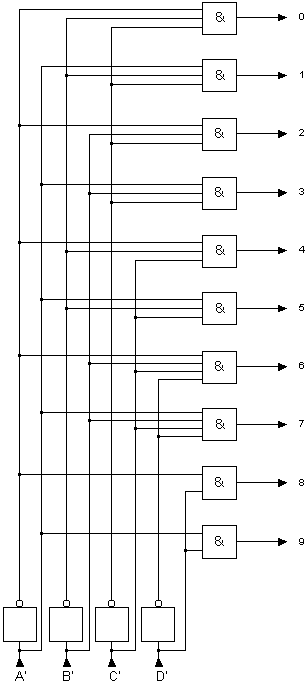
Convertisseur 8421 2421
Si nous observons les codes 8421 et 2421 représentés sur notre premier tableau nous nous apercevons qu'il existe entre eux une importante similitude.
Les positions A et A' ainsi que D et D' sont égales dans les deux cas. Les autres positions ne se distinguent que par les nombres 8 et 9. La conversion du code 8421 en code 2421 se traduit alors par les équivalences logiques suivantes :
A' = A,
B' = B + D,
C' = C + D,
D' = D.
Le circuit logique correspondant est représenté sur la figure suivante :
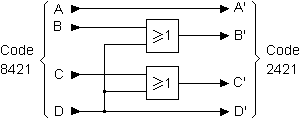
Convertisseur 2421 8421
Les équations logiques pour la conversion du code 2421 en 8421 s'expriment de la même manière :
A = A',
B = B' ⋅ D' + B' ⋅ D' = B' ⊕ D',
C = C' ⋅ D' + C' ⋅ D' = C' ⊕ D',
D = D'.
Avec l'ajout des deux termes B' D' et C' D', il est possible de compléter les équations afin d'utiliser un minimum de composant (fonction OU EXCLUSIF).
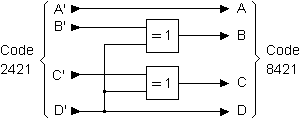
On notera que le code 2421 est un code pondéré.
