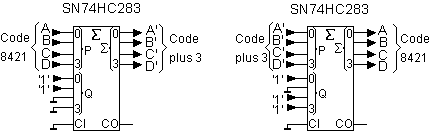
Code plus 3

Le code plus 3 ou code excess 3 appelé aussi code Stibiz du nom de son inventeur, est un code non pondéré issu du code 8421 auquel on ajoute systématiquement 3 à chaque chiffre.
Ce code est souvent utilisé sur des unités arithmétiques qui calculent en système numérique décimal plutôt qu'en système binaire.
Le code plus 3 permet d'effectuer les opérations arithmétiques d'addition et de soustraction avec un minimum de fonctions logiques.
La complexité du code plus 3 pour d'autre applications nous dictera d'utiliser un transcodeur à l'entrée et à la sortie de l'unité arithmétique lorsque celle-ci est utilisée dans uns un système logique complexe.
Le tableau suivant nous présente une comparaison entre le code 8421 et le code plus 3.

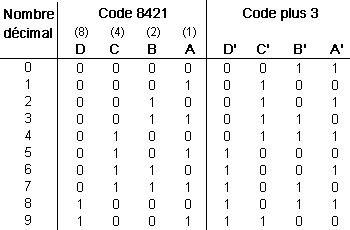
Convertisseur 8421 code plus 3

Le code plus 3 utilise les combinaisons de quatre chiffres du binaire pur compris entre les nombres décimaux 3 et 12.
Chaque nombre s'obtient en ajoutant 3 à chaque chiffre du nombre décimal et en le codant en BCD 8421.
Dans ce système n'apparaissent pas les combinaisons 0000 et 1111. De plus ce code est auto complémentaire.
Exemple : le complément de 7 à 9 est 2
7 = 1010
2 = 0101.

En étudiant la table de vérité, nous allons obtenir les fonctions logiques pour le transcodage BCD 8421 vers le code plus 3.
Equation de A' :
Utilisons un tableau de Karnaugh et reportons les valeurs de A' pour les 9 combinaisons définies dans la table de vérité.
Aux combinaisons non définies nous ferons correspondre le symbole Φ.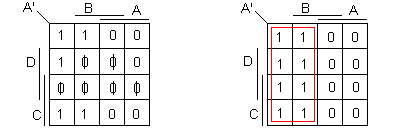

On obtient ici l'expression la plus simple de A' en transformant les Φ des cases 6, 9, 10 en "1" et en transformant le Φ des cases 7, 11, 12 en "0". Le regroupement des cases 1, 2, 5, 6, 9, 10, 13 et 14 nous permet donc d'établir l'équation suivante :
A' = A.

Equation de B' :
Reportons les valeurs de B' dans un tableau de Karnaugh pour les 9 combinaisons valide de la table de vérité.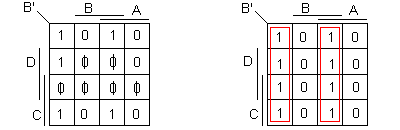

On obtient l'expression simplifiée suivante :
B' = AB + A B
B' = .
Equation de C' :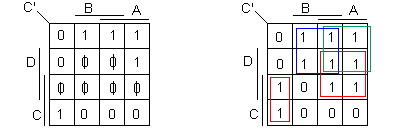

On obtient l'expression simplifiée suivante :
C' = AC + BC + C A B + AD
C' = C (A + B) + C (A + B) + AD
C' = [C (A + B)] + AD
Equation de D' :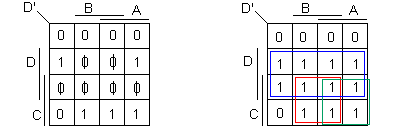

D' = AC + BC + D
D' = C (A + B) + D.

Schéma du circuit convertisseur

En reprenant les équations logiques ci-dessus, nous sommes en mesure d'établir un logigramme pour construire le convertisseur en technologie discrète. Le circuit est complexe à cause du nombre de fonctions logiques différentes mises en oeuvres.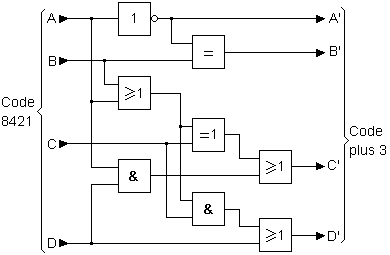

Nous avons vu que pour obtenir un nombre en code plus 3 on ajoute le nombre binaire 3 (0011) à ce nombre correspondant en code 8421.
Exemple :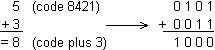

Il est donc possible d'effectuer la conversion en sens inverse en soustrayant le nombre binaire 3 ou bien en ajoutant le nombre binaire 13 (1101).
Un additionneur complet à 4 bits du type SN74HC283 est tout à fait capable de réaliser ce genre d'opération.
Le schéma suivant représente le circuit pour les deux sens de conversion.