Code Gray
Le code Gray est fréquemment utilisé dans les capteurs angulaires ou de positionnement, mais aussi lorsque l'on désire une progression numérique binaire sans parasite transitoire.
Le code Gray sert également dans les tableaux de Karnaugh utilisés lors de la conception de circuits logiques.
Code binaire réfléchi ou code Gray
Le code Gray est un code construit de telle façon qu'a partir du chiffre 0 chaque nombre consécutif diffère du précédent immédiat d'un seul digit.
En l'exprimant autrement nous pouvons également dire que l'on change un seul bit à la fois quand un nombre est augmenté d'une unité.
De plus, nous opèrons de telle manière que le digit de transformation soit d'un poids faible. Si une erreur survient lors d'une transformation d'un nombre à un autre elle est ainsi minimisée.
Commençons par un exemple simple pour les 4 premiers chiffres décimaux 0 à 3.
Rappel de construction du code décimal
Deux bits suffisent et les combinaisons en binaire BCD sont représentées sur l'image suivante :
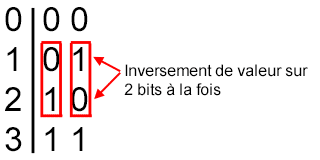
Construction du code décimal : pour la ligne 1 et 2 nous avons inversé 2 bits à la fois.
Nous remarquons que pour aller du nombre 1(10) à 2(10), nous changeons les deux bits à la fois pour passer de 01(2) à 10(2).
Construction du code Gray
En code Gray, pour passer d'une ligne à la suivante, on inverse un seul bit à la fois.
Le choix ce fait sur le bit le plus à droite possible conduisant à un nouveau nombre.
Ce qui donne les combinaisons suivantes :

Construction du code Gray : nous avons inversé 1 bits à la fois.
Recommençons avec les valeur décimales de 0 à 7. Nous avons besoin de 3 bits pour représenter 8 valeur binaires.

Construction du code Gray sur 3 bits.
Construction par la méthode du code binaire réfléchi ou code REFLEX
Le nom code binaire réfléchi vient d'une autre méthode de construction. Elle est plus pratique ou plus visuelle quand au choix du bit à inverser lors du passage d'un nombre au suivant.
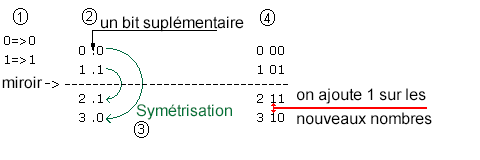
On établi un code de départ : zéro est codé 0 et un est codé 1 (1).
Puis, à chaque fois qu'on a besoin d'un bit supplémentaire (2),
on symétrise les nombres déjà obtenus (comme une réflexion dans un miroir)(3)
et on rajoute un 1 au début des nouveaux nombres (4) et un zéro sur les anciens.
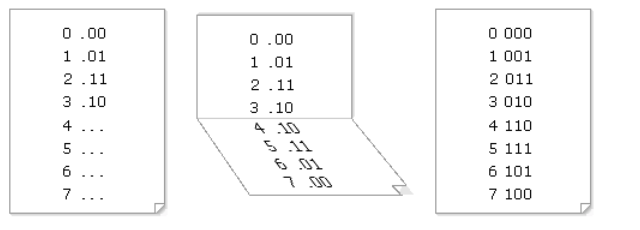
Ci-dessous nous recommençons l'expérience pour les nombres 010 à 710.
Règle de formation du code Gray à partir du binaire pur
Soit un nombre N en binaire pur, pour obtenir son équivalent n en binaire réfléchi, il suffit d'effectuer l'opération suivante : 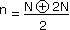
Exemple :
soit N = 0111,
nous avons 2N = 1110 (pour multiplier par 2 on effectue un décalage de la droite vers la gauche).
On effectue maintenant l'opération OU Exclusif de N et 2N :
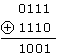
Puis nous divisons par 2 le résultat soit 1001 / 2 = 0100 (pour diviser par 2 on effectue un décalage de la gauche vers la droite).
Nous avons alors :
pour N = 0111 en binaire pur correspond n = 0100 en code Gray.
Les convertisseurs de code
Convertir du binaire au code gray
La construction du code Gray pour les nombres de 0 à 15 est représentée par le tableau suivant :
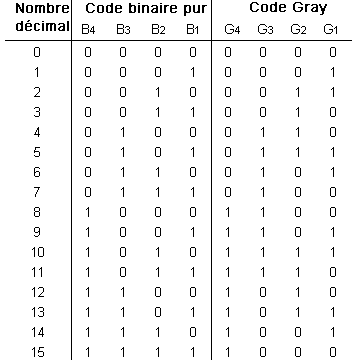
Etablissons un diagramme de Karnaugh pour G1, G2, G3, G4 à partir de B1, B2, B3 et B4.
Les quatre tableaux de Karnaugh permettant d'établir les équations du transcodeur binaire pur vers le code Gray (4 bits).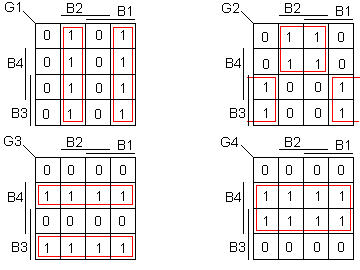
Nous pouvons maintenant établir les équations de G1 à G4 figurant sur l'image suivante :
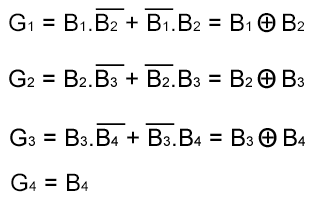
Equations issues du tableau de Karnaugh pour un code Gray sur 4 bits.
Nous pouvons remarquer que le passage du binaire pur au code Gray se fait en effectuant une opération OU Exclusif.
Le circuit du transcodeur est très simple. En désignant par Bn (B1 = LSB) un bit quelconque en code binaire pur et par Gn le bit recherché en code Gray, nous avons alors :
Gn=Bn ⨁ B(n+1).
A partir de cette formule, il est tout à fait possible de concevoir sans difficulté le circuit convertisseur représenté ci-dessous.
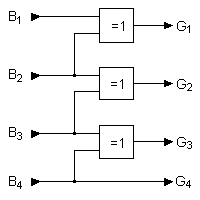
Schéma d'un convertisseur code binaire pur vers code Gray sur 4 bits.
Convertir du code gray en code binaire
Pour la conversion du code Gray en code binaire la relation suivante s'apparente à l'équation vue pour le convertisseur inverse :
Gn=Bn ⨁ B(n+1).
Là encore les fonctions OU Exclusif sont de mise pour la réalisation du circuit de transcodage.
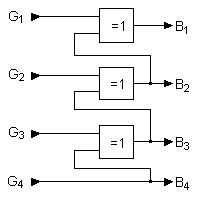
Schéma d'un convertisseur code Gray vers code binaire pur sur 4 bits.
Les circuit représentés ci-dessus peuvent être étendus au nombre de bit nécessaires ou souhaités.
Le code Gray en pratique
Ce code est surtout utilisé pour des capteurs de positions absolue , par exemple sur des règles optiques ou un codeur angulaire solidaire d'un arbre.
En effet, si on utilise le code binaire pur, pendant le passage de la position cinq (101)2 à six (110)2 (changement simultané de 2 bits) il y a un risque de passage transitoire par quatre (100)2 ou sept (111)2, ce que le code Gray évite.
On remarquera que le passage du maximum (quinze sur 4 bits) à zéro se fait également en ne modifiant qu'un seul bit.
Ceci permet par exemple d'encoder un angle, comme la direction d'une girouette ou la position d'un axe sur une machine automatique ou un robot.
Pour la construction d'un codeur angulaire solidaire d'un axe il faut de préférence établir des ensembles de position angulaire multiples d'une puissance de 2 (2, 4, 8, 16, 32…) si l'on veut que le changement du nombre le plus élevé du groupe vers le nombre le plus faible se fasse avec un seul bit.
Pour une girouette à huit position (0=Nord, 1=Nord-Est, 2=Est, … 7=Nord-Ouest) le passage de Nord-Ouest à Nord se fait également sans problème en ne changeant qu'un seul bit.
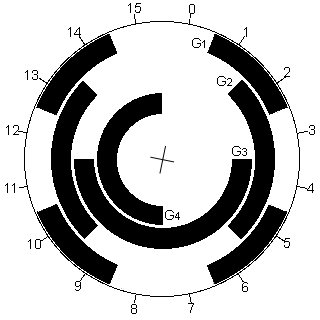
Exemple d'une roue codeuse Gray avec un tracé des pistes noires sur 4 bits.
Nous avons 16 positions angulaires détectées en 4 bits. La lecture s'effectue par 4 cellules photosensibles.
