La fonction logique NAND (NON ET)

L'obtention de la fonction NAND se fait avec 2 variables au moins.
Elle correspond à V₁₄ du tableau des 16 fonctions à 2 variables.

Fonction ET-NON (NAND)

Table de vérité

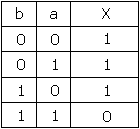
Considération 1

La fonction X prend une valeur inverse de 1 (0) quand l'une et l'autre des variables sont à 1.

Nous l'écrivons : X = a | b.

Nous lirons : X égale a NAND b.

La comparaison avec la fonction ET nous montre que :
la fonction NAND est le complément de la fonction ET
soit : a | b = a ⋅ b.

Considération 2

La fonction X prend une valeur 1 quand l'une ou l'autre des variables sont à l'inverse de 1.

Nous écrirons donc X = a | b = a + b.

Ces deux considérations signifient que :
X = a | b = a ⋅ b = a + b.

Nous verrons plus en détail cette égalité dans l'étude des lois de De Morgan.

Propriétés particulières

a ⋅ 1 = a
a ⋅ 0 = 1
a ⋅ a = a
a ⋅ ¬a = 1

Symbolisation

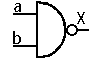
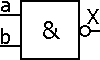
Forme canonique

X = a ⋅ b

Chronogramme

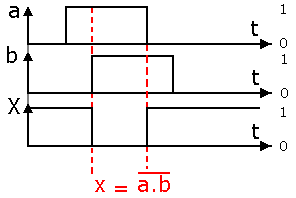
Réalisations pratiques

Exemples de composants en technologie discrète :

• cicuits intégrés en technologie CMOS : 4011, 4012, 4023, 4068, 4093;
• cicuits intégrés en technologie TTL : 7400, 7401, 7403, 7410, 7430, 74133.

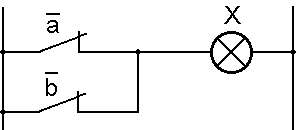
Réalisation électrique