La fonction logique inhibition
La fonction inhibition s'obtient avec deux variables au moins.
Elle correspond à V4 du tableau des 16 fonctions à 2 variables.
Fonction INHIBITION
Table de vérité
| b | a | X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
La fonction X aura une valeur égale à 1 quand a vaudra 1 ET b sera égal à 0.
Nous l'écrivons : X = a ⋅ b
La fonction X présente une valeur inverse de 1 tant que b vaut 0, pour n'importe quelle valeur de a.
Le changement de la variable a est inhibée par la valeur 1 de b (changement de la valeur de X impossible).
Nous l'écrivons : X = a ↑ b
La comparaison avec la fonction IMPLICATION nous montre que :
la fonction INHIBITION est le complément de la fonction IMPLICATION :
a ↑ b = a ⇒ b.
En appliquant les propriétés de De MORGAN nous pouvons écrire :
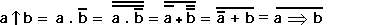
Remarque : la fonction inhibition est universelle.
Symbolisation

Forme canonique
X = a ⋅ b = a 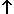 b
b
Chronogramme
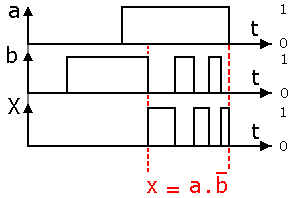
Réalisation électrique
La fonction inhibition est très utilisée en électrotechnique dans les schémas de câblage des circuits
de commande de démarrage de moteurs. En effet, nous avons un dispositif à arrêt prioritaire ;
la priorité est donnée à l'arrêt de la machine si l'on actionne les deux contacts (a et b) simultanément.
