Les fonctions logiques universelles
Une fonction est universelle lorsqu'elle permet, à elle seule, d'exprimer les fonctions de base OUI, NON, ET, OU.
Pour une meilleur compréhension de la suite du cours il est préférable d'étudier les propriétés de l'algèbre de Boole et les lois de De Morgan.
Les fonctions universelles
La fonction OU-NON (NOR) est universelle
En nous aidant de la table de vérité, observons les logigrammes suivants et écrivons leurs expressions résultantes :
Fonction a NOR b 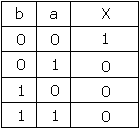
Les deux entrées de notre fonction NOR étant excitées par la même variable, la table de vérité sera simplifiée. Nous ne tiendrons pas compte des cas ou a 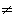 b car les deux entrées de notre fonction seront
toujours au même niveau.
b car les deux entrées de notre fonction seront
toujours au même niveau.
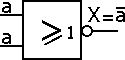
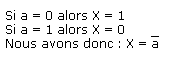
La fonction que nous venons de "fabriquer" est une fonction NON.
Sachant cela nous pouvons écrire que a = a 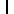 a.
a.
Dans la pratique nous la dessinons et l'utilisons de la manière suivante :
 X = a
X = a
Pour obtenir une fonction OUI :
Nous écrivons : a = a 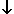 a
= (a
a
= (a 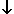 a)
a) 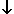 (a
(a 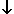 a).
a).
Nous construisons le logigramme suivant :
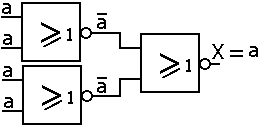
et nous le simplifions pour une utilisation plus pratique :
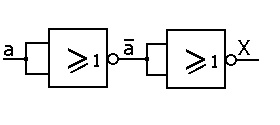
Pour obtenir une fonction ET :
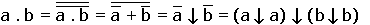
Nous traçons le logigramme correspondant suivant :
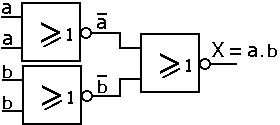
Pour obtenir une fonction OU :
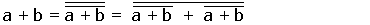
mais aussi :
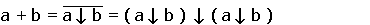
Nous traçons le logigramme correspondant suivant :
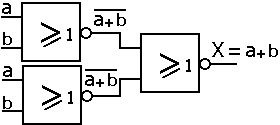
et nous le simplifions pour une utilisation plus pratique :
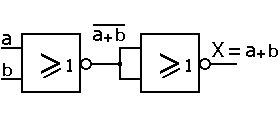
Résumé :
La fonction universelle OU-NON (en anglais : NOR contraction de NOT OR) est le complément de la
fonction OU.
Pour deux entrées a et b la sortie S vaut :
S = a 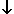 b
b
= a + b
= a ⋅ b
Pour transformer une expression en écriture NOR, nous utilisons les expressions :
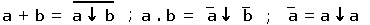
La fonction ET-NON (NAND) est universelle
En nous aidant de la table de vérité et de la démarche précédente , nous pouvons écrire les
expressions résultantes suivantes :
Fonction a NAND b 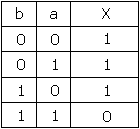
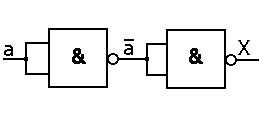
Fonction NON : a = a | a
 X = a
X = a
Fonction OUI : a = a | a = (a | a ) | (a | a)
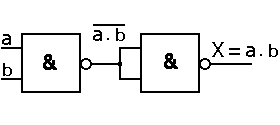
Fonction ET : a ⋅ b = a | b = (a | b) | (a | b)
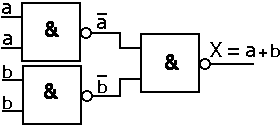
Fonction OU : a + b = a | b = (a | a) | (b | b)
La fonction universelle ET-NON (en anglais : NAND contraction de NOT AND) est le complément de la fonction ET.
Pour deux entrées a et b la sortie S vaut :
S = a | b
= a ⋅ b
= a + b
Pour transformer une expression en écriture NAND, nous utilisons les expressions :
a ⋅ b = a | b ;
a + b = a | b ;
a = a | a
