Construction des fonctions logiques

Du fait qu'une variable logique ne peut prendre que 2 valeurs (0 ou 1), le nombre de fonctions s'en trouve limité.

Fonction à 1 variable logique

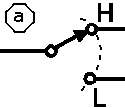
Représentons cette variable par un commutateur-inverseur appelé «a».
En position «L», nous lui attribuons la valeur 0,
en position «H», nous lui attribuons la valeur 1.

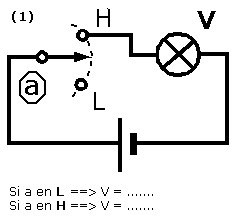
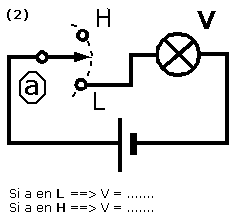
Pour chacun des schémas suivants, donner l'état du voyant V (fonction) en prenant :
V = 1 si le voyant est allumé,
V = 0 si le voyant est éteint.

 
 

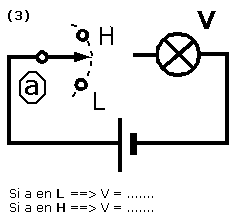
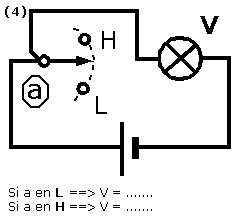
Ce qui nous donne le tableau de synthèse suivant :

Il n'y a pas d'autres combinaisons possibles.

Fonction à 2 variables logiques

Soit a et b les variables logiques pouvant être représentées par 2 commutateur-inverseurs indépendants.

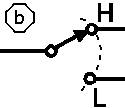
En considérant tout d'abord ces 2 commutateurs ensemble, les 4 combinaisons possibles de commutation sont :

Remplaçons :
la position «L» par la valeur 0,
la position «H» par la valeur 1.

Nous obtenons le tableau suivant

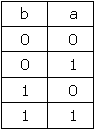
Examinons maintenant les différentes fonctions possibles que nous pouvons obtenir à partir de ces 2 variables.
Les différentes façons de brancher ces 2 commutateurs pour allumer un voyant V conduisent au tableau suivant :
(valeur 0 si éteint),
(valeur 1 si allumé)

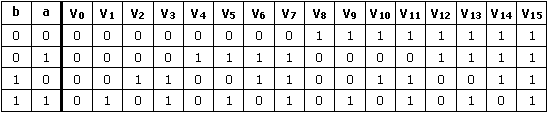
Remarque : chacune des 16 fonctions (V₀ ⇒ V₁₅) prend une valeur qui dépend de la combinaison choisie parmi les 4 des variables a b.

Commentons les différentes fonctions suivantes :

V₀ : le voyant est toujours à 0 ; quelle que soit la position des interrupteurs a et b,
V₁₅ : le voyant est toujours à 1 ; quelle que soit la position des interrupteurs a et b,
V₁ : le voyant est allumé si a et b sont en position : 1,
V₈ : le voyant est allumé si a et b sont en position : 0,
V₃ : le voyant est allumé si b est en position : 1 ; indépendant de la position de a,
V₅ : le voyant est allumé si a est en position : 1 ; indépendant de la position de b.

V₇ : le voyant est allumé si

• a est en position 1,
• ou b est en position 1,
• ou (a et b) sont en position 1.

V₉ : le voyant est allumé si

• a et b sont à : 1,
• ou a et b sont à : 0,
• mais pas si a ≠ b en même temps.

V₆ : le voyant est allumé si

• a est à 1,
• ou b est à 1,
• mais pas si a = b en même temps.

Fonction à n variables logiques

En examinant les deux cas précédents, nous obtenons :
pour 1 variable ⇒ 2 combinaisons ⇒ 4 fonctions,
pour 2 variables ⇒ 4 combinaisons ⇒ 16 fonctions

Ainsi pour n variable ⇒ 2ⁿ combinaisons ⇒ 2⁽²ⁿ⁾ fonctions

Exemples

3 variables ⇒ 8 combinaisons ⇒ 256 fonctions,
4 variables ⇒ 16 combinaisons ⇒ 65 536 fonctions